Способ. Решение однородных тригонометрических уравнений

Математика ПАР-65

Обращаю ваше внимание, на то, что этот урок – пректический. Здесь рассматривается 10 способов решения тригонометрических уравнений. Это все необходимо законспектировать!

Решение тригонометрических уравнений. Способы их решения.

Сегодня мы с вами рассмотрим более сложные тригонометрические уравнения. Рассмотрим 10 способов их решения. Итак, переходим к рассмотрению способов решения тригонометрических уравнений. Одни из этих способов вам, наверное, покажутся трудными, а другие – лёгкими, т.к. некоторыми приёмами решения уравнений вы уже владеете.

Способ. Решение уравнений разложением на множители

sin 4x = 3 cos 2x

Для решения уравнения воспользуемся формулой синуса двойного угла

sin 2 = 2 sin cos
2 sin 2x cos 2x – 3 cos 2x = 0,
cos 2x (2 sin 2x – 3) = 0.

 Произведение этих множителей равно нулю, если хотя бы один из множителей будет равен нулю.

2x = + к, к Z или sin 2x = 1,5 – нет решений,

т.к | sin | 1
x = + к; к Z.
Ответ: x = + к, к Z.

Способ. Решение уравнений преобразованием суммы или разности тригонометрических функций в произведение

cos 3x + sin 2x – sin 4x = 0.

Для решения уравнения воспользуемся формулой

sin – sin = 2 sin сos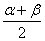

cos 3x + 2 sin сos = 0,

сos 3x – 2 sin x cos 3x = 0,

cos 3x (1 – 2 sinx) = 0. Полученное уравнение равносильно совокупности двух уравнений:

Множество решений второго уравнения полностью входит во множество решений первого уравнения. Значит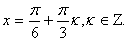

Ответ: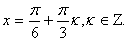

 3 способ. Решение уравнений преобразованием произведения тригонометрических функций в сумму

sin 5x cos 3x = sin 6x cos2x.

Для решения уравнения воспользуемся формулой

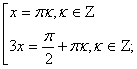
Ответ:

Способ. Решение уравнений, сводящихся к квадратным уравнениям

3 sin x – 2 cos²x = 0,
3 sin x – 2 (1 – sin²x) = 0,
2 sin²x + 3 sin x – 2 = 0,

Пусть sin x = t, где | t | . Получим квадратное уравнение 2t² + 3t – 2 = 0,

D = 9 + 16 = 25.

. Таким образом . не удовлетворяет условию | t | .

Значит sin x = . Поэтому .

Ответ:

способ. Решение однородных тригонометрических уравнений

Уравнения вида a sin x + b cos x = 0, где a и b – некоторые числа, называются однородными уравнениями первой степени относительно sin x или cos x.

Рассмотрим уравнение

sin x – cos x = 0. Разделим обе части уравнения на cos x. Так можно сделать, потери корня не произойдёт, т.к., если cos x = 0, то sin x = 0. Но это противоречит основному тригонометрическому тождеству sin ² x + cos ² x = 1.

Получим tg x – 1 = 0.

tg x = 1,

Ответ:

Уравнения вида a sin ² x + bcos ² x + c sin x cos x = 0, где a, b, c – некоторые числа, называются однородными уравнениями второй степени относительно sin x или cos x.

Рассмотрим уравнение

sin²x – 3 sin x cos x + 2 cos² = 0. Разделим обе части уравнения на cos x, при этом потери корня не произойдёт, т.к. cos x = 0 не является корнем данного уравнения.

tg² x – 3tg x + 2 = 0.

Пусть tg x = t. D = 9 – 8 = 1.

тогда 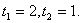Отсюда tg x = 2 или tg x = 1.

В итоге x = arctg 2 + , x =

Ответ: arctg 2 + ,

Рассмотрим ещё одно уравнение: 3 sin²x – 3 sin x cos x + 4 cos² x = 2.
Преобразуем правую часть уравнения в виде 2 = 2 · 1 = 2 · (sin²x + cos²x). Тогда получим:
3sin²x – 3sin x cos x + 4cos² x = 2 · (sin²x + cos² x),
3sin²x – 3sin x cos x + 4cos²x – 2sin²x – 2 cos²x = 0,
sin²x – 3sin x cos x + 2cos²x = 0. (Получили 2 уравнение, которое уже разобрали).

Ответ: arctg 2 + k,