Обобщение и систематизация знаний

Восточная мудрость

Цели и задачи урока:

1) повторить основные формулы и методы решения тригонометрических уравнений;

Личностные результаты: сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

Метапредметные результаты: умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в обучении;

Предметные результаты: осознание значения математики для повседневной жизни человека; 

Тип: урок обобщения и систематизации знаний                                                                    

Ход урока

Организационный момент.

Презентация

Слайд 1

- Французский математик и физик Паскаль говорил: “Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным”.

Я предлагаю вам разгадать такой ребус.

Слайд 2

- Как вы думаете, почему я предложила вам расшифровать такое слово? Что оно означает?

Слайд 3

“Тригонометрия” происходит от греческого слова τριγουο треугольник и греческого μετρειν измерять, т.е. означает измерение треугольников. Тригонометрия - это раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

Мотивация учебной деятельности.

- Одной из наиболее важных тем тригонометрии является решение тригонометрических уравнений, с которыми мы познакомились в этом учебном году. Эта тема очень актуальна и важна, т.к. входит в вопросы переводного экзамена в 10 кл. и широко представлена на ЕГЭ в 11 кл.

Итак, тема сегодняшнего урока “Решение тригонометрических уравнений”.

Актуализация знаний

Слайд 4. “Решение тригонометрических уравнений”.

Слайд 5

Восточная мудрость гласит: “Приобретать знания - храбрость, приумножать их - мудрость, а умело применять - великое искусство”

Какие-то знания по теме “Тригонометрические уравнения” мы уже приобрели, приумножать знания - никогда не поздно, поэтому и на сегодняшнем уроке будем мудрыми, и еще раз посмотрим, насколько умело мы применяем наши знания.

Чтобы решить любое тригонометрическое уравнение, что необходимо знать?

- Общие формулы решения простейших тригонометрических уравнений.

- Какие простейшие тригонометрические уравнения вы знаете?

- sin x = a, cos x = a, tg x = a, ctg x = a.

- Вспомните общие формулы их решений.

1. ,   

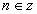
2.

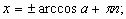
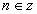
3.

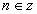
4.

 

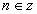
Слайд 6

Простейшие тригонометрические уравнения sin x = a, cos x = a

- Что надо помнить при решении таких уравнений?

- Частные случаи. Слайд 7

Слайд 8

Уравнения вида tg x = a и ctg x = a.

- Проверим, насколько хорошо мы умеем решать простейшие тригонометрические уравнения.

Укажите общую формулу, по которой находятся все корни уравнения. Слайд 9

Вариант I

1)

А) ,

Б) ,

В) Корней нет,

Г) ,

Д) .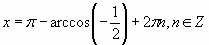

Ответ: А), Г)

2)

А) ,

Б) ,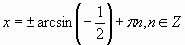

В) ,

Г) Корней нет,

Д) .

Ответ: В).

Вариант II

1)

А) ,

Б) ,

В) ,

Г) ,

Д)

Ответ: В).

2)

А) ,

Б)

В)

Г) ,

Д) .

Ответ: А), В).

Слайд 10

Проверьте себя! (Указаны правильные ответы).

Обобщение и систематизация знаний

- Решение простейших уравнений мы вспомнили, можно приступать к решению более сложных уравнений.

Вспомним, какие методы тригонометрических уравнений мы знаем.

Наверное, надо начать с общих методов:

- разложение на множители,

- метод введения новой переменной,

К специальным методам относятся:

- применение формул тригонометрии,

- метод вспомогательного аргумента,

- метод универсальной подстановки.

Слайд 11

1. .

- Метод?

- Введение новой переменной (у = sin х) Получим уравнение: 2 +у-1=0; Д=1-4·2·(-1)=9;

=-2, 1

sin х=-2 нет решения, sin х=1;  х= +2

Слайд 12

2.

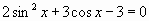
- Сведение к квадратному уравнению относительно cos x.

,подставим в уравнение и решаем путём введения новой переменной у=COSX

Слайд 13

3.

- Применение формул тригонометрии, разложение на множители.

 Нужно вынести за скобки sin х, получим: sin х (2cosx+1)=0 и решим 2 уравнения: sin х=0; (2cosx+1)=0

Слайд 14

4.

- Сведение к одноименным функциям, сведение к квадратному уравнению.

 Получим уравнение: 4tgx - 3·  -1 = 0. Упростим и получим уравнение

4  x – tgx – 3 = 0. Введем подстановку y = tgx. Получим квадратное уравнение: 4  – у – 3 =0

Дальше решаете как предыдущее.

Слайд 15

5.

- Как называется такое уравнение и как его решить?

- Однородное II степени: cos² x 0 Разделим почленно на x

Сведение к квадратному уравнению относительно tg.

Слайд 16

=> - корень уравнения.

5. Информация о домашнем задании. Повторить п. 36 и решить все уравнения до конца, которые в конспекте урока

Рефлексия

При подведении итога урока мне хочется задать вам один вопрос: что бы вы посоветовали ученику, который только начинает учиться решать тригонометрические уравнения?

Начните свои советы со слов: “Помни, что…”.

И в конце нашего урока хочу обратить ваше внимание на такие слова Станислава Коваля “Уравнение - это золотой ключ, открывающий все математические сезамы”.

Слайд 28

Спасибо за урок!