Содержание.
Введение
1. Логорифмы
1.1. История возникновения логарифмов
1.2. Свойства логарифма
1.3. Натуральные логарифмы
1.4. Десятичные логарифмы
2. Комплексный логарифм
2.1. Риманова поверхность
2.2. Логарифмические таблицы
Заключение
Список использованных источников
Введение.
В этом реферате хочу рассказать об таком великом открытии в математике, как логарифм. Когда не было вычислительной техники, сложные вычисления отнимали много времени и сил. Неизбежны были и ошибки. И ученные путем проб и ошибок нашли решение этой проблемы.
Виды логарифмов.
1.1. История возникновения логарифмов
Логарифмы возникли в 16 веке в связи с необходимостью проведения большого объема приближенных вычислений в ходе решения практических задач, и в первую очередь задач астрономии, (в частности, при определении положения судов по звездам и по Солнцу).Потребность в сложных расчётах в XVI веке быстро росла. Значительная часть трудностей была связана с умножением и делением многозначных чисел. В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n.В предисловии к книге «Рабдология» Непер писал:
Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.
Сам термин «ЛОГАРИФМ» предложил Дж. Непер; он возник из сочетания греческих слов logos (здесь — отношение) и arithmos (число),которое означало “число отношений”.
Логарифмы с основанием ввел учитель математики Спейдел. Слово основание заимствовано из теории о степенях и перенесено в теорию логарифмов Эйлером. Глагол “логарифмировать” появился в 19 веке у Коппе. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов. Обозначения, близкие к современным ввел немецкий математик Прингсхейм в 1893 году. Именно он обозначал логарифм натурального числа через ln. Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).
В 1614 году шотландский математик-любитель Джон Неперопубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов» (лат. Mirifici Logarithmorum Canonis Descriptio). В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1’. Термин логарифм, предложенный Непером, утвердился в науке.
Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение; например, логарифм синуса он определил следующим образом
Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать.
К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.
В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.
Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.
Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.
Свойства логарифма.
Свойства логарифмов. Десятичный логарифм. Натуральный логарифм.
Логарифмом положительного числа N по основанию (b > 0, b 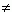 1) называется показатель степени x, в которую нужно возвести b, чтобы получить N. Обозначение логарифма: 1) называется показатель степени x, в которую нужно возвести b, чтобы получить N. Обозначение логарифма:  Эта запись равнозначна следующей: bx = N. П р и м е р ы: log 81 = 4, так как 34 = 81; log 27 = – 3, так как (1/3) -3 = 33 = 27. Вышеприведенное определение логарифма можно записать в виде тождества: Эта запись равнозначна следующей: bx = N. П р и м е р ы: log 81 = 4, так как 34 = 81; log 27 = – 3, так как (1/3) -3 = 33 = 27. Вышеприведенное определение логарифма можно записать в виде тождества:  Основные свойства логарифмов. 1) log b = 1, так как b 1 = b. 2) log 1 = 0, так как b 0 = 1. 3) Логарифм произведения равен сумме логарифмов сомножителей: log (ab) = log a + log b. 4) Логарифм частного равен разности логарифмов делимого и делителя: log (a / b) = log a – log b. 5) Логарифм степени равен произведению показателя степени на логарифм её основания: log (b k) = k · log b. Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня: Основные свойства логарифмов. 1) log b = 1, так как b 1 = b. 2) log 1 = 0, так как b 0 = 1. 3) Логарифм произведения равен сумме логарифмов сомножителей: log (ab) = log a + log b. 4) Логарифм частного равен разности логарифмов делимого и делителя: log (a / b) = log a – log b. 5) Логарифм степени равен произведению показателя степени на логарифм её основания: log (b k) = k · log b. Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:  6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак логарифма: 6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак логарифма:  Два последних свойства можно объединить в одно: Два последних свойства можно объединить в одно: 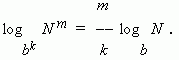 7) Формула модуля перехода (т.e. перехода от одного основания логарифма к другому основанию): 7) Формула модуля перехода (т.e. перехода от одного основания логарифма к другому основанию):  В частном случае при N = a имеем: В частном случае при N = a имеем: 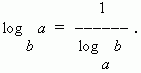 1.3. Натуральные логарифмы. Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln, т.е. log e N = ln N. Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число (1 + 1 / n) n при неограниченном возрастании n (см. так называемый второй замечательный предел в разделе "Пределы"). Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию. 1.3. Натуральные логарифмы. Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln, т.е. log e N = ln N. Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число (1 + 1 / n) n при неограниченном возрастании n (см. так называемый второй замечательный предел в разделе "Пределы"). Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию. |
Графики логарифмических функций.
Логарифм числа b по основанию a (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число»[1]) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: 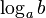 . Из определения следует, что записи
. Из определения следует, что записи  и
и 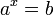 равносильны.
равносильны.
Пример:  , потому что
, потому что  .
.
Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg, т.е. log 10 N = lg N. Логарифмы чисел 10, 100, 1000,... pавны соответственно 1, 2, 3, …, т.е. имеют столько положительных единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001,... pавны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей (считая и нуль целых). Логарифмы остальных чисел имеют дробную часть, называемую мантиссой. Целая часть логарифма называется характеристикой. Для практического применения десятичные логарифмы наиболее удобны.
Логарифм вещественного числа logab имеет смысл при 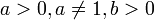 .
.
Наиболее широкое применение нашли следующие виды логарифмов.
Десятичные: 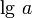 , основание: число 10.
, основание: число 10.
Натуральные:  , основание: e (число Эйлера).
, основание: e (число Эйлера).
Двоичные: 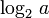 или
или  , основание: число 2. Они применяются в теории информации и информатике.
, основание: число 2. Они применяются в теории информации и информатике.
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию, например:  . Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема там (см. рис. 1).
. Эта функция определена в правой части числовой прямой: x > 0, непрерывна и дифференцируема там (см. рис. 1).
Логарифмическая функция.
Логарифмической функцией называется функция вида f (x) = logax, определённая при 
Исследование логарифмической функции
Область определения: 
Область значения: 
График любой логарифмической функции проходит через точку (1;0)
Производная логарифмической функции равна:
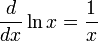

 2020-05-21
2020-05-21 971
971







