Если, кроме того, выполнено условие

Практическая работа № 29.

Тема: Вычисление пределов последовательностей.

Цель: Применение знаний и формул к вычислению последовательностей

Теория.

Предел числовой последовательности

Определение 1. Число a называют пределом числовой последовательности

a ₁ , a ₂ , … a_n, …

если для любого положительного числа ε найдется такое натуральное число N, что при всех n > N выполняется неравенство

| a_n – a | < ε.

Условие того, что число a является пределом числовой последовательности

a ₁ , a ₂ , … a_n, …,

Записывают с помощью обозначения

и произносят так: «Предел a_n при n, стремящемся к бесконечности, равен a».

То же самое соотношение можно записать следующим образом:

a_n → a при .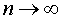

Словами это произносится так: «a_n стремится к a при n, стремящемся к бесконечности».

Замечание. Если для последовательности

a ₁ , a ₂ , … a_n, …

найдется такое число a, что a_n → a при 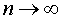, то эта последовательность ограничена.

Определение 2. Говорят, что последовательность

a ₁ , a ₂ , … a_n, …

стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N, что при всех n > N выполняется неравенство

| a_n | > C.

Условие того, что числовая последовательность

a ₁ , a ₂ , … a_n, …,

Стремится к бесконечности, записывают с помощью обозначения

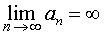
Или с помощью обозначения

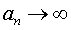при .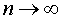

Пример 1. Для любого числа k > 0 справедливо равенство

Пример 2. Для любого числа k > 0 справедливо равенство

Пример 3. Для любого числа a такого, что | a | < 1, справедливо равенство

Пример 4. Для любого числа a такого, что | a | > 1, справедливо равенство

Пример 5. Последовательность

– 1, 1, – 1, 1, …,

Заданная с помощью формулы общего члена

a_n = (– 1) ⁿ,

Предела не имеет.

Свойства пределов числовых последовательностей

Рассмотрим две последовательности

a ₁ , a ₂ , … a_n, …, и b ₁ , b ₂ , … b_n, ….

Если при 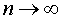существуют такие числа a и b, что

и ,

то при 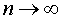существуют также и пределы суммы, разности и произведения этих последовательностей, причем

	,
	,
	.

Если, кроме того, выполнено условие

,

то при 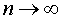существует предел дроби

, причем

 Для любой непрерывной функции f (x) справедливо равенство