Биномиальное распределение вероятностей

Группа П-19 (Задание 3) Математическая статистика (16.04.2020)

1. Изучить теорию

2. Решить задачу (номер задачи соответствует номеру в журнале).

Биномиальное распределение вероятностей

Или биномиальный закон распределения вероятностей. Исходя из моих наблюдений и личной статистики – это наиболее распространённый вид дискретного распределения, с которым мы уже встречались добрый десяток раз.

Я буду формулировать задачу в общем виде и попутно приводить конкретный пример:

Пусть проводится n независимых испытаний (не обязательно повторных), в каждом из которых случайное событие A может появиться с вероятностью p. Тогда случайная величина X – число появлений события A в данной серии испытаний, имеет биномиальное распределение.

Совершенно понятно, что эта случайная величина может принять одно из следующих значений: .

Например: монета подбрасывается 5 раз. Тогда случайная величина X – количество появлений орла распределена по биномиальному закону. Орёл обязательно выпадет:

или  раз, или , или , или , или , или  раз.

Как вы догадались, соответствующие вероятности определяются формулой Бернулли:

, где:

n – количество независимых испытаний;

p – вероятность появления события A в каждом испытании;

q=1-p – вероятность непоявления события A в каждом испытании;

 – сколько раз может появиться событие  в данной серии испытаний (список всех возможных значений).

Сведём этот закон распределения в таблицу:

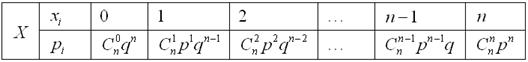
Вероятности  представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. По формуле бинома:

,

что мы и ожидали увидеть.     В нашем примере с монеткой:

 – вероятность того, что в 5 испытаниях орёл не выпадет вообще ();

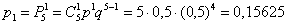 – … ровно  раз;

 – вероятность того, что в 5 испытаниях орёл выпадет ровно  раза;

 – … ровно  раза;

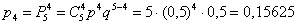 – … ровно  раза;

 – … ровно  раз.

Таким образом, закон распределения числа выпавших орлов:

Контроль: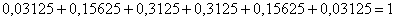

Легко видеть, что нахождение биномиального ряда распределения – есть занятие муторное, и это хорошо, если он содержит 3-4-5-6 значений. А ведь немало задач, где требуется рассчитать 8-10, а то и бОльшее количество вероятностей!

Поэтому вычисления целесообразно автоматизировать в Экселе с помощью его стандартной функции:

=БИНОМРАСП(m; n; p; 0), где m количество успехов в n испытаниях, а p – вероятность успеха в каждом испытании.

Задача. Вероятность поражения цели при одном выстреле равна 0,6. Составить закон распределения случайной величины X – числа попаданий в цель при четырех выстрелах. Вычислить M(X) и D(X). Построить многоугольник и функцию распределения. Найти P(|X-M(X)|<σ(X)).

Решение: по существу, текст условия совпадает с Задачей статьи о геометрическом распределении, но есть одно принципиальное отличие – здесь другая случайная величина. А именно, под страхом расстрела совершается серия из n=4 и строго из 4 выстрелов, вероятность попадания в каждом из которых составляет p=0,6.

Очевидно, что испытания независимы, и случайная величина  распределена по биномиальному закону.

Составим ряд распределения данной случайной величины. Используем формулу Бернулли:  для  – всех возможных результатов рассматриваемой серии.

На этом шаге я сразу забью n=4, p=0,6 в свой расчётный макет (Пункт 6), чтобы контролировать правильность каждого пункта. Для удобства их можно нумеровать:

0)           – вероятность того, что в 4 выстрелах не будет попаданий;

1)           – вероятность того, что в 4 выстрелах будет ровно 1 попадание;

2)          – … ровно 2 попадания;

3)           – … ровно 3 попадания;

4)          – … ровно 4 попадания.

Таким образом, искомый закон распределения:

Проверка: , ч.т.п.

Пока таблица не ушла из поля зрения, построим многоугольник распределения: Вычислим математическое ожидание и дисперсию. И тут есть отличная новость – для биномиального распределения можно не использовать общий алгоритм расчёта этих числовых характеристик – по той причине, что существуют готовые формулы:

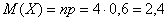 – среднеожидаемое количество попаданий;

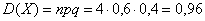 – рассеяние количества попаданий относительно матожидания.

Всегда бы так!

Составим функцию распределения вероятностей: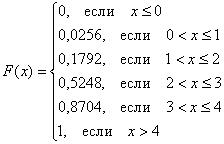

Я не буду вновь останавливаться на алгоритме её построения, и если что-то не понятно, то смотрите по ссылке выше. Раз ступенька, два ступенька – будет график:

Найдём P(|X-M(X)|<σ(X)). – вероятность того, что значение случайной величины X отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение.

Среднее квадратическое отклонение: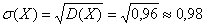

и искомая вероятность:

Как вариант, в разобранной задаче может быть предложена другая случайная величина: не количество попаданий, а X – количество промахов. Нетрудно догадаться, что в этом случае вероятности «развернутся наоборот» , и числовые характеристики с графиками будут другими.

Задачи: (можно присылать фотографии, но лучше сделать задание по ИТ и присылать *.xls файлы).

1.В хоре Африканского 5 теноров, каждый из которых на концерте «даёт петуха» с вероятностью 0,2. X – число теноров, поющих без нареканий.   Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	2. Пять полицейских, показывающих одинаковые результаты в беге, гнались за одним жуликом. Вероятность того, что жулик убежит от полицейского 0,1. X – количество полицейских, догнавших жулика. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
3.Зубной врач вырывает зуб с первой попытки с вероятностью 0,4. Пациенту надо вырвать 5 зубов. Если зуб не удалось вырвать с первой попытки, пациент второй попытки вырвать этот зуб врачу уже не даст. X – количество вырванных зубов у пациента. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	4.В поисках Царевны-лягушки Иван-царевич обследовал 5 болот. Вероятность того, что он найдет в каждом из болот Царевну-лягушку, которую надо поцеловать, равна 0,6. X – количество поцелованных Иваном-царевичем лягушек. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
5.В трамвай вошли 5 человек. Вероятность того, что проездной билет будет опознан системой АСКП, установленной в трамвае, равна 0,5. X – количество человек, вынужденных ехать в тамбуре. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	6. Вероятность того, что каждый из пяти участников, претендующих на рекорд Гиннесса, съест килограмм гуталина за час равна 0,9. X – количество участников, недоевших свой килограмм гуталина. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
7.Вероятность того, что каждый из пяти приглашенных принесет Леночке в подарок на день рождения котенка, равна 0,8. X – количество подаренных котят.   Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	8.Изобретатель-самоучка изобрел пятиколёсный велосипед и поехал на нем в магазин. Вероятность отказа каждого из колес равна 0,7. X – количество уцелевших колес. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
9.Для выкапывания картошки на дачном участке тётя Клава купила пять лопат. Черенок лопаты ломается с вероятностью равной 0,5. X – количество лопат, уцелевших до следующего сезона. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	10.Вася взял у соседки по даче пять куриных яиц, положил их в авоську и побежал домой. Вероятность того, что яйцо разобьётся при подобной транспортировке, равна 0,3. X – количество яиц, доставленных домой. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
11.Вася взял пять куриных яиц и стал, стоя за забором, закидывать их в открытую форточку Леночке. Вася обычно закидывал с этого расстояния картофелины и стабильно попадал 7 раз из 10бросков. X – количество яиц, достигших цели. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	12. Тетя Клава решила покататься на лодке и взяла на лодочной станции пять вёсел, поскольку она знает, что весла ломаются с вероятностью равной 0,6. X – количество весел, возвращенных на лодочную станцию целыми. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
13.Вася перепрыгивает лужу с вероятностью 0,4. От подъезда Васиного дома его отделяет всего пять луж. X – количество луж, которые Васе не удалось перепрыгнуть. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	14.Тёте Клаве необходимы придверные коврики на дачу. Свой она везти не хочет. В подъезде живут еще 5 семей, которые с вероятностью 0,9 надежно приклеили коврики к полу. X – число ковриков, добытых тётей Клавой Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .
15.Охранник собрал 5 канализационных люков и пошел сдавать их в ближайший пункт приема вторсырья. Оказалось, что там принимают только люки «МГТС». Вероятность того, что люк принадлежит МГТС равна 0,2. X – число люков, которые придётся нести в другой пункт приёма. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .	16.Если охранник ударит неисправным электрошокером коллегу, тот выстоит и даст сдачи с вероятность 0,8. Охранник рискнул ударить 5 коллег. X – число ударенных коллег, которым не удалось дать сдачи охраннику. Составить ряд распределения случайной величины X, построить полигон распределения, найти функцию распределения F(x), нарисовать её график, вычислить M(X), D(X), Ϭ(X), .