ПРАКТИЧЕСКАЯ РАБОТА №2
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Теоретическая часть
Определение: Пусть функция f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число А называется пределом функции f(x) в точке а (или при х, стремящемся к а), если для любых значений аргумента (х¹а) изсколь угодно малой окрестности точки а, последовательность соответствующих значений функции f(x) мало чемотличается от А (т.е. f(x) приближенно равны А).
В этом случае пишут 
Свойства пределов:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:  ,
,
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют:  ,
,
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
 ,
,
Теорема 4: Предел отношений двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
 ,
,
2. Примеры:
1) Предел многочлена.
Пример. Вычислить 
Решение: 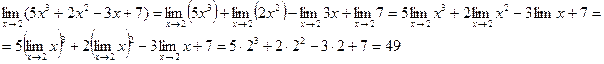
Таким образом, для вычисления предела многочлена f (x) при x → x0 достаточно
вместо переменной x подставить значение x0, к которому она стремится, и выполнить соответствующие действия, т.е. 
2) Предел отношения двух многочленов,  , где x0 – число.
, где x0 – число.
а) Если g (x0) ≠ 0, то можно применить теорему о пределе частного.
Пример. Пусть требуется вычислить 
Решение: Здесь f (x) = x 3 – 2 x – 3 и g (x) = x 2 + 3 x + 3. Т.к g (3) = 32 + 3 ∙ 3 + 3 = 21 ≠ 0. то имеем: 
5
б) Если g (x0) = 0, то теорему о пределе частного применить нельзя. Тогда если ƒ(x0) = A ≠ ≠ 0, то 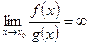 , если же ƒ (x0) = 0 – то имеем неопределённость вида (0/0). В этом случае предел
, если же ƒ (x0) = 0 – то имеем неопределённость вида (0/0). В этом случае предел  можно вычислить разложением многочленов ƒ(x) и g(x) на множители.
можно вычислить разложением многочленов ƒ(x) и g(x) на множители.
Пример. Вычислить  .
.
Решение: здесь ƒ (2) = 22 - 5∙2 + 6 = 0, g (2) = 22 - 6∙2 + 8 = 0. Так как x ≠ 2, имеем
 .
.
3) Пределы некоторых иррациональных функций. Для вычисления 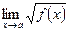 ,
,
где ƒ (x) ≥ 0 и  , воспользуемся равенством
, воспользуемся равенством
 ,
,
которое принимается нами без доказательства. Например,
 .
.
Пример. Вычислить  .
.
Решение: Так как  , то теорему о пределе частного применить нельзя. Умножая числитель и знаменатель на выражение, сопряжённое знаменателю, получим
, то теорему о пределе частного применить нельзя. Умножая числитель и знаменатель на выражение, сопряжённое знаменателю, получим
 44) Предел функции на бесконечности
44) Предел функции на бесконечности
Пример 1. Вычислить  .
.
Решение:
 .
.
Пример 2. Вычислить 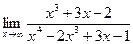 .
.
 .
.
Пример 3. Вычислить  .
.
Решение: 
Требования к содержанию отчета по работе
Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
 2020-05-21
2020-05-21 87
87






