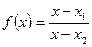| Теоретические факты | Фронтальная работа | Базовые конструкции (основные типы задач) | |||||||
| 1. Решение линейных неравенств Линейное неравенство – это неравенство вида ax +b > 0 (илиax +b < 0), где а и b – любые числа, причем а ≠ 0. Решением неравенствас одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Например, х + 5 < 17. Подставив вместо х значение 1, получим 1+ 5 < 17, 6 < 17 –верное числовое неравенство. Значит, х = 1 –решение данного неравенства. Решить неравенство– это значит найти все его решения или доказать, что решений нет. Свойство числовых неравенств Если а > b и m > 0, то аm > bm; Если а > b и m < 0, то am < bm. | Алгоритм решения линейных неравенств
5(х – 3) > 2х - 3
1. Раскрыть скобки 5х – 15 > 2х – 3
2. Перенести все слагаемые с х влево, а числа вправо, меняя при этом знак на противоположный:
5х – 2х > -3 + 15
3. Привести подобные слагаемые: 3х > 12.
4. Разделить обе части неравенства на число, стоящее перед х (если это число положительное, то знак неравенства не меняется; если это число отрицательное, то знак неравенства меняется на противоположный)
3х > 12: 3 х > 4
5. Перейти от аналитической модели х > 4 к геометрической модели:
 6. Указать множество решений данного неравенства, записав ответ:
Ответ: (4; +∞)
6. Указать множество решений данного неравенства, записав ответ:
Ответ: (4; +∞)
|
Решите неравенство 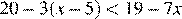 .
В ответе укажите номер правильного варианта.
1) .
В ответе укажите номер правильного варианта.
1) 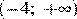 2)
2) 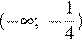 3)
3) 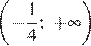 4)
4) 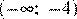 Решение.
Решим неравенство:
Решение.
Решим неравенство:
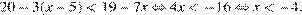 Правильный ответ указан под номером 4.
Правильный ответ указан под номером 4.
| |||||||
| 2. Решение квадратных неравенств 2.1. Графический метод | Алгоритм решения квадратных неравенств
Общий вид квадратных неравенств, это ax2+bx+c>0 (<0,≤0,≥0), где a≠0.
Шаги решения квадратного неравенства:
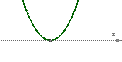
1. Определяются точки пересечения параболы и оси x с помощью решения уравнения ax2+bx+c=0.
Вспомним формулы корней квадратного уравнения:
D=b2−4ac
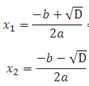
2. Учитывая количество корней и знак коэффициента a, чертится график параболы. Обрати внимание! Если a>0, ветви параболы устремлены вверх, если a<0, то вниз.
Совет: если хочешь, чтобы ветви параболы всегда были уcтремлены вверх, в случаях, когда a<0, сначала обе части неравенства перемножь на (−1). Не забудь, что на противоположный поменяется также знак неравенства.
3. Выбираются пустые или закрашенные точки, в зависимости от вида знака неравенства: ∙, если стоит знак нестрогого неравенства ≤ или ≥ о, если стоит знак строгого неравенства < или >
4. Закрашивается правильный интервал.
5. Записывается ответ. |
1. Решить x2–15x+50 > 0
Первый этап.
Решаем квадратное уравнение
x2–15x+50=0
D = b2–4ac = (–15)2–4∙1∙50 = 225–200 = 25
Находим корни:
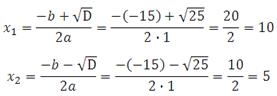 Второй этап.
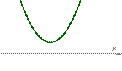
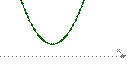
Строим ось ох. Отмечем полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х2 положительный:
Второй этап.
Строим ось ох. Отмечем полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х2 положительный:
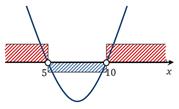 Третий этап.
Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать.
Записываем ответ.
2. Решить квадратное неравенство −2x2+4x−5≤0
Решение:
Третий этап.
Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать.
Записываем ответ.
2. Решить квадратное неравенство −2x2+4x−5≤0
Решение:
| |||||||
| 2.2 Метод интервалов | Алгоритм решения квадратных неравенств методом интервалов таков: · 1. Находим нули квадратного трехчлена a·x2+b·x+c из левой части квадратного неравенства. · 2. Изображаем координатную прямую и при наличии корней отмечаем их на ней. Причем если решаем строгое неравенство, то отмечаем их пустыми (выколотыми) точками, а если решаем нестрогое неравенство – то обычными точками. Они разбивают координатную ось на промежутки. · 3. Определяем, какие знаки имеют значения трехчлена на каждом промежутке и · проставляем над этими промежутками + или − в соответствии с определенными знаками. · Если решаем квадратное неравенство со знаком > или ≥, то наносим штриховку над промежутками со знаками +, если же решаем неравенство со знаком < или ≤, то наносим штриховку над промежутками со знаком −. В результате получаем геометрический образ некоторого числового множества, которое и является искомым решением неравенства. · Записываем ответ. | Пример 1. Решить неравенство: 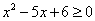 . Разложим квадратный трехчлен на сомножители. . Разложим квадратный трехчлен на сомножители. 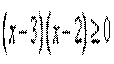  Неравенство примет вид: Построим чертеж. Неравенство примет вид: Построим чертеж. 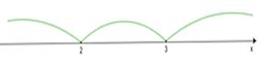 Рассмотрим эти интервалы в том же порядке, как пишем и читаем: слева направо. 1) х
Рассмотрим эти интервалы в том же порядке, как пишем и читаем: слева направо. 1) х 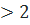 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение. Например: . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение. Например: 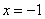
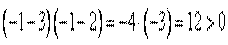 2) 2 2) 2 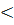 х х 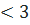 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение. Например: . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение. Например: 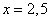 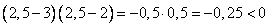 3) 3) 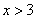 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение. Например: . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение. Например: 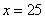 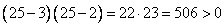 Внесем эти данные в чертеж. Внесем эти данные в чертеж.  Точки, удовлетворяющие неравенству обозначаются закрашенными, а неудовлетворяющие – незакрашенными. Точки, удовлетворяющие неравенству обозначаются закрашенными, а неудовлетворяющие – незакрашенными.  Окончательный ответ: Окончательный ответ: 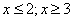 Пример 2: Решить неравенство
Пример 2: Решить неравенство 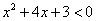 . Краткое оформление решения: . Краткое оформление решения: 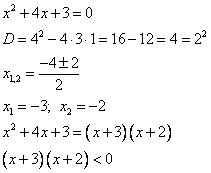 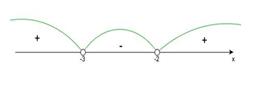 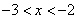 Ответ: Ответ: 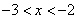 . .
| |||||||
| 3. Рациональные неравенства | Алгоритм решения дробно- рациональных неравенств методом интервалов. 1. 2. Область допустимых значений 3. Нули функции 4. Определяем интервалы знакопостоянства. 5. Расставим знаки на промежутках(самостоятельно можно проверить знаки методом пробной точки) 6. Выбрать интервалы, удовлетворяющие заданным условиям.
| Решить неравенство:
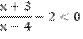 Эквивалентными преобразованиями приведем неравенство к нужному виду.
Эквивалентными преобразованиями приведем неравенство к нужному виду.
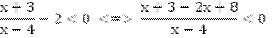
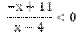
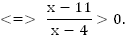 Множество решений этого неравенства совпадает со множеством решений исходного неравенства
Неравенство такого вида мы уже умеем решать методом интервалов.
1.
Множество решений этого неравенства совпадает со множеством решений исходного неравенства
Неравенство такого вида мы уже умеем решать методом интервалов.
1. 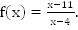 2. Область допустимых значений
2. Область допустимых значений 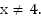 3. Нули функции
3. Нули функции 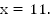 4. Определяем интервалы знакопостоянства.
4 – выколотая точка, т.к. при
4. Определяем интервалы знакопостоянства.
4 – выколотая точка, т.к. при 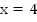 функция не существует, изобразим это на графике пунктирной линией.
5. Расставим знаки на промежутках. Самостоятельно можно проверить знаки методом пробной точки (Рис.2). функция не существует, изобразим это на графике пунктирной линией.
5. Расставим знаки на промежутках. Самостоятельно можно проверить знаки методом пробной точки (Рис.2).
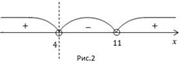 Теперь можно вернуться к неравенству и выбрать интервалы, удовлетворяющие заданным условиям.
Ответ:
Теперь можно вернуться к неравенству и выбрать интервалы, удовлетворяющие заданным условиям.
Ответ: 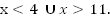 Мы привели исходное неравенство к дробно-линейному виду.
Мы привели исходное неравенство к дробно-линейному виду.
|
 2020-05-21
2020-05-21 353
353
 ,
парабола пересекает ось x в двух точках
,
парабола пересекает ось x в двух точках