Рациональные, иррациональные, показательные и тригонометрические неравенства

 

       Теоретический материал

       Определение 1.     Неравенства, имеющие одно и то же множество решений, называют равносильными.

При решении неравенств обычно данное неравенство преобразуется в ему равносильное.

Например, неравенство (х - 3)/(х² + 1) < 0 и х - 3 < 0 равносильны, т.к. имеют одно и то же множество решений: х < 3. Неравенства 2х/(х - 1) > 1 и 2х > х - 1 не равносильны, т.к. решениями первого являются решения х < -1 и х > 1, а решениями второго - числа х > -1.

       Определение 2. Область определения неравенства - это множество таких значений х, при которых имеют смысл обе части неравенства.

       Неравенства сами по себе представляют интерес для изучения, т.к. именно с их помощью на символическом языке записываются важнейшие задачи познания реальной действительности. Часто неравенство служит важным вспомогательным средством, позволяющим доказать или опровергнуть существование каких-либо объектов, оценить их количество провести классификацию. Поэтому, с неравенствами приходится сталкиваться не менее часто, чем с уравнениями.

Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.

Рациональное выражение - это алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.

Решение всех рациональных неравенств сводится к двум основным шагам:

Шаг 1. Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.

Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.

Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.

Шаг 2. Метод интервалов.

В отличие от уравнений, в неравенствах мы никогда не разделяем числитель и знаменатель! Более того, если в числителе и знаменателе есть одинаковые нечисловые множители, мы их не сокращаем!

Определение. Неравенство, содержащие переменную под знаком корня, называется иррациональным.

Пример 1. √(5 - х) < 4. Устно проводится рассуждение, затем записывается решение. При обсуждении учащимся задаются вопросы:

- Какова область определения неравенства?

- При каком условии при возведении в квадрат обеих частей получится равносильное неравенство?                   

                       5 - х ≥ 0

√(5 - х) < 4 <=>  5 - х < 16 <=> -11 < х ≤ 5.

Показательными называются неравенства, в которых неизвестное содержится в показателе степени.

Основные свойства степеней, при помощи которых преобразуются показательные неравенства, перечислены в теоретических материалах по теме 7 «Показательные уравнения».Кроме того, пользуются также следующими свойствами показательной функции у = а^х,

a > 0; а 1

1) а^x > 0 при всех а > 0 и x R;

2) при а > 1 функция у= а^х возрастает, т.е. если a>1 и <=> x₁ > x₂;

3) при 0< a < 1 функция у = а^х убывает, т.е. если 0 < a < 1 и <=> x₁ < x₂.

Неравенства: sin x > a, sin x a, sin x < a, sin x a

Sin x > a arcsin a + 2 n < x < – arcsin a + 2 n, n Z

= arcsin a; = – arcsin a.

sin x<a – – arcsin a + 2 n<x< arcsin a + 2 n, n Z

= – – arcsin a; = arcsin a.

В случае нестрогих неравенств знаки < и > в решениях заменяются соответственно на и .

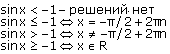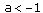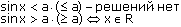Во всех приведенных здесь формулах n Z.

Неравенства:

cos x> a; cos x a; cos x < a; cos x a.

В случае нестрогих неравенств знаки < и > в решениях заменяются соответственно на и .

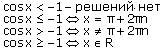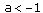Во всех приведенных здесь формулах n Z.

Неравенства:

tg x > a; tg x a; tg x < a; tg x a.

Вопросы для составления опорного конспекта (письменно ответить)

1. Какие неравенства называются равносильными?
2. Область допустимых значений неравенств?
3. Какие неравенства называются рациональными?
4. Способ решения рациональных неравенств?
5. Какие неравенства называются иррациональными?
6. Какие неравенства называются показательными?
7. Какие неравенства называются тригонометрическими?