2020-05-21
385
Практическая работа
Выполнение действий над векторами
Цель работы: закрепить умения выполнять действия над векторами
Содержание работы.
Основные понятия.
1 Вектором называется отрезок, у которого указано, какой из концов является началом, а какой – концом (направленный отрезок), обозначается 
, 
, где 
- начало вектора, 
- конец.
2 Векторы называются коллинеарными, если они расположены на одной или параллельных прямых.
3 Векторы называются ортогональными, если угол между ними 
.
4 Векторы можно складывать (по правилам треугольника и параллелограмма), можно умножать на число: 
; 
.
5 Необходимое и достаточное условие коллинеарности векторов: 
6 Модуль вектора 
равен 
7 Если заданы начало 
и конец 
вектора 
, то его координаты и длина находятся следующим образом:
; 
.
8 Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними
9 
10 Необходимое и достаточное условие ортогональности векторов: 
.
11 Проекция вектора на направление: 
|
|
|
Задание
1 Найти линейную комбинацию векторов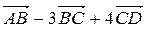 
2 Найти длины векторов 
3 Найти косинусы углов между векторами 
4 Найти Найти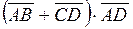 
5 Найти 
6 Выяснить, коллинеарны ли векторы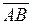 
и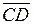 
7 Выяснить, ортогональны ли векторы 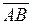и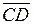
Исходные данные:
Даны точки 
.
Задание 1
Решение:
Задание 2
Решение:
Задание 3
Решение:
Задание 4
Решение:
Даны точки 
.
Задание 5
Решение:
,
, 
,
.
.
Задание 6
Решение:
, 
векторы не являются коллинеарными.
Задание 7
Решение:
, 
, следовательно, векторы не являются ортогональными.
ИНСТРУКЦИОННАЯ КАРТА
для проведения практической работы
Тема занятия: выполнение действий над векторами
Цель выполнения задания: закрепить умения выполнять действия над векторами
Необходимо знать: основные формулы и правила работы с векторами
Необходимо уметь: применять основные формулы и правила работы с векторами
Оборудование (приборы, материалы, дидактическое обеспечение): методические рекомендации к выполнению работы; задание и инструкционная карта для проведения практического занятия
Теория: для выполнения заданий по данной теме необходимо предварительно изучить теоретические материалы, а также методические рекомендации к выполнению работы
Порядок выполнения задания, методические указания: - ознакомиться с теоретическими положениями по данной теме; - изучить схему решения задач; - выполнить задания практической работы; - сформулировать вывод
Содержание отчета: отчет по практической работе должен содержать: основные определения, рассуждения по решению задач, необходимые вычисления, ответ; вывод по работе
|
|
|
Контрольные вопросы:
1 Чем характеризуется вектор?
2 Какие операции можно производить над векторами?
3 Какие векторы называются равными?
4 Что можно сказать об угле между векторами, если скалярное произведение отрицательно?
5 Что можно сказать об угле между векторами, если скалярное произведение положительно?
6 Что можно сказать об угле между векторами, если их скалярное произведение равно нулю?
7 Какие векторы называются коллинеарными?
8 Условие коллинеарности векторов
9 Какие векторы называются ортогональными?
10 Условие ортогональности векторов
11 Скалярное произведение векторов
12 Проекция вектора на направление
13 Координаты вектора
14 Длина вектора
