Урок №5 «Синус и косинус, тангенс суммы и разности двух аргументов»
Цели урока: 1. Изучить формулы синус, косинус и тангенс суммы и разности двух аргументов
2. Научиться применять эти формулы для решения задач
Формулы синуса и косинуса суммы двух аргументов
На уроке рассматриваются формулы синуса и косинуса суммы аргументов, применение этих формул для решения некоторых задач на вычисление и упрощение выражений, решение уравнений и доказательство тождеств.
Самыми важными в тригонометрии являются следующие две формулы:
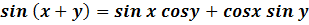

Применение формул синуса и косинуса суммы двух аргументов для разных задач
1. Задача: Вычислить 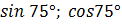 .
.
Решение:
1) Применяя формулу синуса суммы двух углов, имеем:
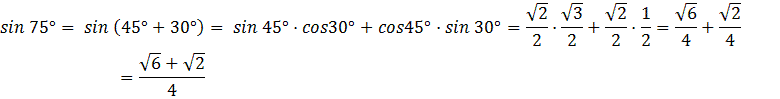
2) Применяя формулу косинуса суммы двух углов, имеем:
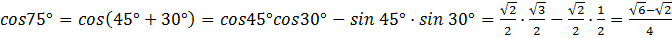 .
.
Ответ: 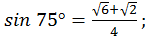

2. Задача: упростить выражение 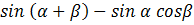 .
.
Решение: применяя формулу синуса суммы двух аргументов, получаем:
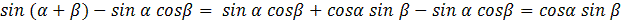 .
.
Ответ: 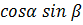 .
.
В следующей задаче используется формула косинуса суммы двух аргументов.
3. Задача: упростить выражение
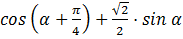 .
.
Решение:

Ответ: 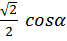 .
.
Доказательство тождеств с помощью формул синуса и косинуса суммы двух аргументов
4. Доказать тождество:
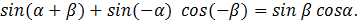
Доказательство:
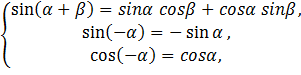
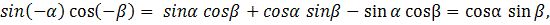
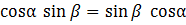 ,
,
что и требовалось доказать. Все действия можно провести и в обратном порядке.
5. Доказать тождество: 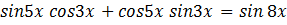 . (1)
. (1)
Доказательство:
Пусть 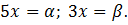
1) Докажем, что левая часть равна правой части:
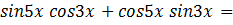

2) Можно доказать, что правая часть равна левой части:

Получим
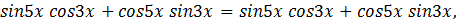
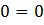
при всех 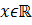 .
.
При этом, (1) эквивалентно верному равенству при всех действительных 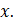 Тождество доказано.
Тождество доказано.
Вычислительные задачи
6. Найдите значение выражения: 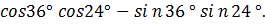
Решение:
Используя формулу 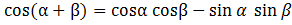 при
при 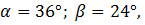 получаем:
получаем:
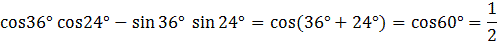 .
.
Ответ:  .
.
7. Вычислить:
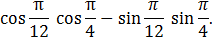
Решение:
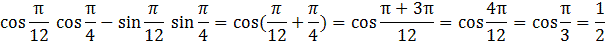 .
.
Ответ:  .
.
8. Задача.
Дано:
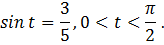
Вычислить:
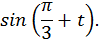
Вычисление:
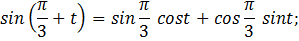
из основного тригонометрического тождества имеем:
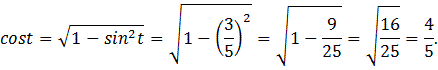
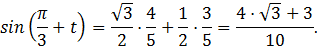 Ответ:
Ответ: 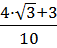 .
.
Теперь рассмотрим формулы синуса и косинуса разности двух аргументов.

 6. Итог урока
6. Итог урока
На уроке рассматривались формулы синуса, косинуса и тангенса суммы и разности аргументов, их применение для решения некоторых задач.
Домашнее задание:
1.Математика: алгебра и начала математического анализа, геометрия. 10-11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни/ [ Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.].-4-е изд.-М.: Просвещение, 2017
Гл.5, параграф 28, выполнить №№ 482-486 (четные)
2. Выполнить практическую работу:
- Вычислить:
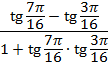 ;
; 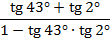
- Найти
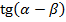 , если
, если  ;
; 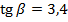 .
. - Вычислить:
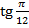 ;
; 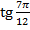
 2020-05-21
2020-05-21 181
181






