2020-05-21
174Урок №16,17 от 22.04.2020
· Изучите §11 п. 11.3 С. 303 - 306 «Применение основных тригонометрических формул для решения уравнений».
Рекомендации: для лучшего понимания темы просмотрите видео, конспект, дополнительные материалы, а также выполните задания на сайте https://resh.edu.ru/
Ø Тригонометрические уравнения
https://resh.edu.ru/subject/lesson/6314/start/199928/
Ø Методы решения тригонометрических уравнений
https://resh.edu.ru/subject/lesson/6320/start/200020/
· Оформите в тетради (перепишите или распечатайте и вклейте) решение следующих заданий:
Решите уравнения:
1) 
2) 
3) 
4) 
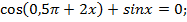
5) 
6) 
1) 
Применим формулу основного тригонометрического тождества: 
и выразим 
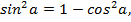
Введём замену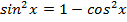 
в данном уравнении и перепишем уравнение:
Решим полученное уравнение:
Введём замену 
и перепишем уравнение: 
,
Решим данное уравнение (по основной формуле) и получим: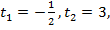 
Вернёмся к замене:
1) 
, 
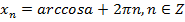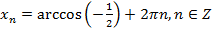и 
,
и 
,
и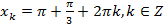 
,
и 
,
и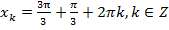 
,
и 
,
и 
,
2) 
, так как 
, то уравнение не имеет корней.
Ответ: , .
2) 
Применим формулу синуса суммы двух углов: 
к данному уравнению, с учётом того, что здесь 
и перепишем его:
,
Решим уравнение: , 
,
Введём замену 
и перепишем уравнение: 
,
Решим полученное уравнение: 
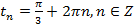и 
,
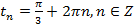и 
,
и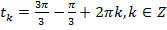 
,
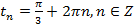и 
,
и 
,
Вернёмся к замене: 
или 
,
Решим оба уравнения:
1) , 
,
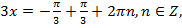
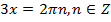Разделим всё уравнение на 3:
,
2) , 
, 
,
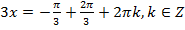Разделим всё уравнение на 3:
.
Ответ: , .
3) 
Применим формулу косинус двойного угла 
к данному уравнению и перепишем его: 
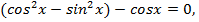
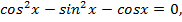
Применим формулу основного тригонометрического тождества: и выразим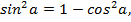
Введём замену 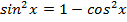в данном уравнении и перепишем уравнение:
Решим полученное уравнение: 
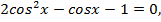
Введём замену и перепишем уравнение: 
,
Решим данное уравнение (по основной формуле) и получим: 
Вернёмся к замене:
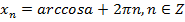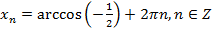1) , и ,
и ,
и ,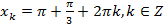
и ,
и ,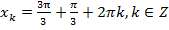
и ,
и ,
2) 
, решение данного уравнения можно определить по тригонометрическому кругу (косинус соответствует оси 
, 
в точке 
); 
;
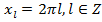Ответ: , , .
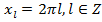4) 
Применим формулу косинуса суммы двух углов: 
к данному уравнению,
, и перепишем исходное уравнение 
:
Применим формулу синуса двойного угла к этому уравнению: 
и перепишем уравнение: 
Вынесем общий множитель за скобки: 
Тогда или 
Решим оба уравнения:
1) 
решение данного уравнения можно определить по тригонометрическому кругу (синус соответствует оси 
, 
в точках и 
); 
;
2) 
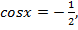
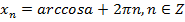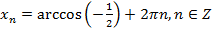и ,
и ,
и ,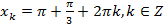
и ,
и ,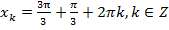
и ,
и ,
Ответ: , , .
5) 
Применим формулу косинус двойного угла к данному уравнению и перепишем его: 
,
;
Применим формулу основного тригонометрического тождества: 
к данному уравнению и перепишем его: 
,
, 
;
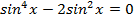Вынесем общий множитель за скобки: 
Тогда или 
Решим оба уравнения:
1) 
тогда 
, решение данного уравнения можно определить по тригонометрическому кругу (синус соответствует оси , в точках и );
;
2) 
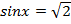, тогда или 
, или 
, так как 
, то оба этих уравнение не имеют корней;
Ответ: .
6) 
Применим формулу квадрат суммы 
к сумме 
: 
, выразим 
из этого выражения, тогда 
,
но по основному тригонометрическому тождеству: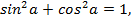 
тогда
,
то есть 
;
Подставим полученное выражение в исходное уравнение и перепишем его:
;
Возведём обе части формулы синуса двойного угла в квадрат, то есть
, 
, 
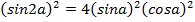, выразим 
из этого выражения, тогда 
;
Подставим полученное выражение в уравнение и перепишем его:
, 
,
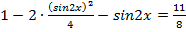Умножим всё уравнение на 8:
, 
,
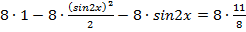Введём замену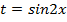 
, и перепишем уравнение: 
, 
;
Решим данное уравнение (по основной формуле) и получим: 
Вернёмся к замене:
1) 
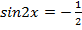, введём замену 
и перепишем данное уравнение: 
;
Решим данное уравнение:
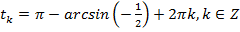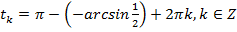и ,
и 
,
и 
,
и 
,
и 
,
и 
,
и 
,
Вернёмся к замене: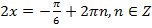 
или 
,
Разделим каждый член каждого уравнения на 2:
или 
;
2) 
, так как 
, то оба этих уравнение не имеют корней.
Ответ: , .
· Выполните домашнее задание.
Домашнее задание:
1) С. 299 – 302 §11 п. 11.2 читать внимательно
2) Выполнить задание на карточке
Карточка
Решить уравнения:
1) 
2) 
3) 
4) 
5) 
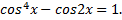
· Домашнее задания оформите в тетради.
· Сфотографируйте в разборчивом виде.
· Передайте мне до 24.04.2020 через эл.дненик, Whatsapp, или VK.
Критерии оценивания заданий карточки
Каждое уравнение может быть оценено в:
1) 1 балл, если решение верное, записан верный ответ;
2) 0,5 балла, если в решении допущена одна вычислительная ошибка (ошибки в формулах к вычислительным не относятся) и с учётом этой ошибки решении верное, записан верный ответ; или если есть одна ошибка в обосновании решения; или если решение верное, но не записан или записан неверный ответ;
3) 0 баллов – во всех случаях не указанных в пунктах 1 и 2.
Баллы суммируются. Максимальное количество баллов – 5.
Перевод баллов в оценки
5 баллов – оценка «5»
от 4 до 4,5 баллов – оценка «4»
от 2,5 до 3,5 баллов – оценка «3»
менее 2,5 баллов – оценка «2»
