2020-05-25
98
В простейшем варианте рассматриваемые случайные объекты являются случайными величинами, принимающими лишь конечное число значений.
Пусть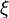 
и 
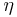– случайные величины, принимающие 
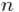и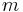 
различных значений с вероятностями 
и 
соответственно. Тогда количество информации, содержащейся в с.в. 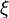относительно с.в. 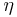определяется числом
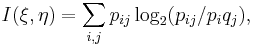
где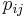 
вероятность пересечения событий « 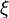принимает 
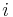-е значение» и « 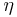принимает 
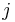-е значение».
Информация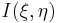 
обладает рядом свойств, которые естественно требовать от числовой меры информации. Так, всегда 
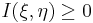и равенство 
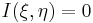возможно тогда и только тогда, когда 
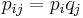при всех 
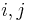, т. е. когда случайные величины 
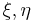независимы. Далее, всегда 
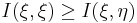и равенство возможно только в случае, когда 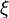есть функция от 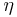(напр., 
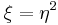и т. д.). Справедливо равенство 
– мера информации 
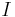симметрична относительно своих аргументов. Кроме того, количество информации 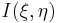не зависит от значений с.в. 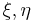, а только – от распределения их вероятностей.
Величина
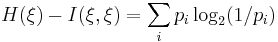
носит название энтропии случайной величины 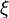. Понятие энтропии относится к числу основных понятий теории информации. Количество информации и энтропия связаны соотношением
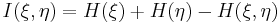
где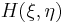 
— энтропия пары 
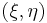, т. е.
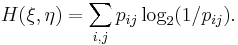
Величина энтропии указывает среднее число двоичных знаков, необходимое для различения (записи) возможных значений случайной величины. Это обстоятельство позволяет понять роль количества информации при «хранении» информации в запоминающих устройствах. Основная информационная характеристика каналов, так называемая пропускная способность, определяется через понятие информации.
Есл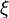и и 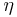могут принимать бесконечное число значений, то предельным переходом получается формула
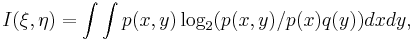
где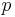 
и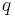 
обозначают соответствующие плотности вероятности. При этом энтропи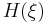и 
и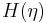 
не существуют, но имеет место аналогичная формула:
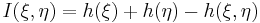
где
____________________________________________________________________
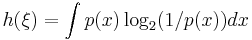
Задание для самоконтроля и самостоятельной работы по теме.
Внимание!
Избегайте бездумного копирования информации
