1) Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
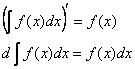
2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
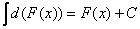
Учитывая, что  , свойство можно переписать в следующем виде:
, свойство можно переписать в следующем виде:
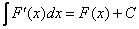
Константу можно вынести из-под знака интеграла
То есть, если  , то
, то 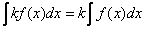
4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
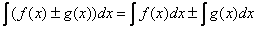
Справедливо для любого количества слагаемых.
Таблица первообразных. Вычисление неопределенных интегралов.
| Функция f(x) | Первообразная F(x) | Пример |
| 0 | С | |
| 1 | х + С | 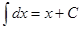
|
| k (свободное число) | kx + C | 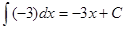
|

| 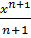 + C + C
| 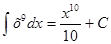
|
| x | 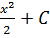
| |
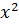
| 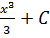
| 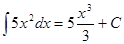
|
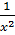
| 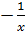 + C + C
| 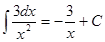
|

| 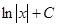
| |
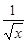
| 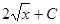
| |

| 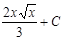
| |
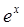
| 
| |

| 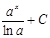
| 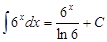
|
| sin x | - cos x +C | |
| cos x | sin x+C | |
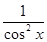
| tg x +C | 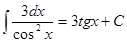
|

| - ctg x+C |
 2020-05-21
2020-05-21 112
112








