Лекция: Первообразная функция, неопределённый интеграл и его свойства

ЭТ-19, Математика,                                                           27.04.2020

Задание:

1. Записать конспект лекции в тетрадь, внимательно разбирая задания.

2. Фото работы отправить по окончании пары до 15.00 в ВК по ссылке: https://vk.com/topic-193913663_41476550   

Лекция:  Первообразная функция, неопределённый интеграл и его свойства

К понятию первообразной функции приводят многие задачи математического анализа и физики. Рассмотрим былинный физический пример: известен закон изменения скорости тела 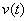, требуется найти закон изменения координаты 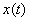данного тела.

Скорость – это производная от пройдённого пути: 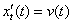, таким образом, для решения задачи необходимо по заданной функции 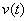(производной) восстановить функцию .

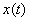Общая же постановка вопроса такова: в распоряжении есть некоторая функция 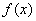и возникает потребность выяснить, от какой функции она произошла. То есть, необходимо найти ТАКУЮ функцию 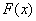, чтобы .

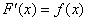Определение: функция 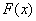называется первообразной для функции 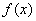на некотором промежутке, если для всех 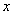из этого промежутка выполняется равенство 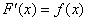или, что то же: .

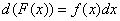Например, для 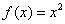первообразной функцией на всей числовой прямой будет являться функция 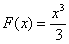. И действительно, для любого «икс»:
.

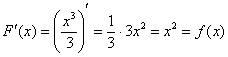Простое, но требующее доказательства утверждение:

Теорема: пусть 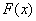– какая-нибудь первообразная для функции 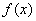на некотором промежутке. Тогда функция 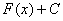, где 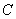– произвольная константа, тоже будет первообразной функцией для 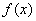на данном промежутке.

Доказательство: поскольку производная константы равна нулю, то:
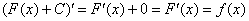, следовательно, 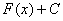– первообразная для функции 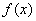по определению первообразной, что и требовалось доказать.

Так, для функции 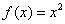первообразной будет являться любая функция из множества 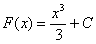, где 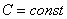(мысленно поподставляйте конкретные числовые значения).

Определение: множество всех первообразных 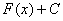для функции 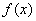называется неопределённым интегралом от функции 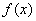и обозначается символом 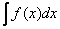. Таким образом, по определению:

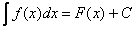, где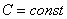

Напоминаю, что функция 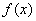называется подынтегральной функцией, 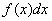– подынтегральным выражением, а сам процесс отыскания множества первообразных 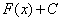– интегрированием.

Интегрирование – это восстановление функции 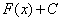по её производной 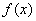(обратное действие по отношению к дифференцированию).

Для нашего демонстрационного примера:
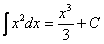, где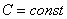

Проверка: 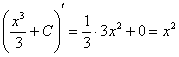– исходная подынтегральная функция.

Любая ли функция интегрируема? Нет.

Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.