Ряды с неотрицательными членами

При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.

Теорема. Для сходимости ряда с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.

Признак сравнения рядов с неотрицательными членами

Пусть даны два ряда с неотрицательными членами  

,             (1)

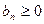,             (2)

Если для любого п, то из сходимости ряда (1) следует сходимость ряда (2) и сумма ряда (2) не превосходит суммы ряда (1); из расходимости ряда (2) следует расходимость ряда (1).

Пример. Исследовать на сходимость ряд

Т.к. , а гармонический ряд  расходится, то расходится и ряд .

Пример. Исследовать на сходимость ряд

Т.к. 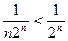, а ряд  сходится (как убывающая геометрическая прогрессия), то ряд  тоже сходится.

Также используется следующий признак сходимости:

Теорема. Если  и существует предел , где h – число, отличное от нуля, то ряды  и ведут одинаково в смысле сходимости.

Признак Даламбера

Пусть дан ряд  с положительным членами.

Если существует предел , то при r < 1 ряд сходится, а при r > 1 – расходится. Если r = 1, то ряд может быть как сходящимся, так и расходящимся.

Пример. Исследовать на сходимость ряд .

. Следовательно, по признаку Даламбера ряд сходится.

Пример. Исследовать на сходимость ряд

. Следовательно, по признаку Даламбера ряд сходится.