Позиционные задачи на кривых поверхностях

Все позиционные задачи на кривых поверхностях решаются каркасным способом, поэтому построение линий каркаса является ключевой задачей этого метода.

Задача 1. Построение каркаса поверхности. В общем случае, когда линии каркаса поверхности являются пространственными кривыми, эта задача может быть  трудоёмкой. Однако на практике чаще используются простейшие каркасы: линейчатый или циклический (см. примеры для задач 2 и 3).

Задача 2. Построить недостающую проекцию линии l, лежащей на поверхности Ф.

Алгоритм решения задачи:

1. Строим каркас поверхности Ф. Линии каркаса располагают произвольно, но с равномерным заполнением поверхности.

2. Отмечаем точки пересечения заданной проекции прямой l, с проекциями линий каркаса.

3. Строим недостающие проекции указанных точек и соединяем их плавной кривой.

В качестве примеров на рис. 86, а показано построение недостающей горизонтальной проекции l₁, а на рис. 86, б – фронтальной проекции l₂ линии l, расположенной на поверхности конуса вращения. В первом случае использован циклический каркас, а во втором случае – линейчатый каркас этой поверхности. При нахождении фронтальной проекции точки 3 (см. рис. 86, б) использована окружность с циклического каркаса.

Задача 3. По заданной проекции точки, лежащей на поверхности Ф, построить недостающую проекцию этой точки.

Алгоритм решения в общем случае:

1. Через заданную проекцию точки проводим одноименную проекцию вспомогательной линии t, расположенной на поверхности Ф.

2. Каркасным способом строим недостающую проекцию этой линии (см. задачу 2)  и на ней находим недостающую проекцию точки.

В качестве примера рассмотрим построение точек А (А₁) и В (В₂), расположенных на поверхности Ф – коноида (см рис. 76), заданного определителем: ГЧ (l, m, ň, a); ÀЧ (l ⁱ çç a; l ⁱ Ç m;

l ⁱ Ç ň; i=1 ¸ k).

Недостающую проекцию А₂ точки А строим проведением через неё линии каркаса l¢ (см. рис. 87, б). Сначала через А₁ проводим l¢₁ çç a₁. Затем по точкам пересечения 1 и 2 строим l¢₂  и на ней находим точку А₂.

Построение недостающей проекции В₁ точки В (см. рис.87, в) нельзя выполнить аналогично точке А, т. к. на плоскости П₂ неизвестно направление линии каркаса, проходящей через эту точку (прямой, параллельной плоскости a). Поэтому сначала на поверхности Ф строим вспомогательную линию t (t₂ ' B₂). Для простоты проекция t₂ проведена в виде прямой линии (плоская кривая). Далее строим произвольный каркас поверхности (l ⁱ; i=1 ¸ 5). Построение линий каркаса l ⁱ следует начать на плоскости проекций П₁, т.к. l₁ⁱ çç a₁. С помощью каркаса по точкам 1 ¸ 5 находим недостающую проекцию t₁ вспомогательной линии t, а на ней -  искомую проекцию В₁ точки В.

Задача 4. Построить фигуру сечения поверхности Ф плоскостью a.

В случае, когда плоскость a, является проецирующей (рис. 88), решение задачи сводится к построению недостающей проекции m₁ линии m, расположенной на поверхности Ф (см. задачу 2), т. к. на эпюре имеется отрезок   m₂ = A₂B₂ – вырожденная проекция фигуры сечения, находящийся на вырожденной проекции a₂ плоскости a и ограниченный линиями изображения поверхности.

При построении замкнутой линии m₁ рекомендуется строить не менее восьми точек.

Рассмотрим пять вариантов сечения конуса вращения плоскостью (рис. 89, 90):

а) сечение по окружности, когда секущая плоскость располагается перпендикулярно оси вращения конуса (a ^ i);

б) сечение по двум образующим, когда плоскость проходит через вершину конуса (a ' S);

в) сечение по эллипсу, когда плоскость не перпендикулярна оси вращения и может пересекать все образующие конуса;

г) сечение по параболе, когда плоскость проходит параллельно одной из образующих конуса (a çç l);

д) сечение по гиперболе, когда плоскость проходит параллельно двум образующим конуса (a çç l, l¢).

Для случая, когда секущая плоскость a занимает общее положение, рекомендуется выполнить преобразование чертежа (например, замену плоскости проекций), чтобы секущая плоскость стала проецирующей (рис. 91).

 Алгоритм построения:

1. Расположив ось новой системы   х₁₄ ^ h₁ (гпг), строим на плоскости П₄ проекцию тора и вырожденную проекцию a ₄ плоскости a. При построении a ₄  можно использовать две вспомогательные точки М и Т.

На плоскости П₄ находим характерные точки: точку А, имеющую z _max, и точки 1, 1 ¢, имеющие    z = 0. Точка А расположена в общей плоскости симметрии g. Эта плоскость проходит через ось вращения тора перпендикулярно горизонтали h плоскости a (см. вырожденную горизонтальную проекцию g₁ этой плоскости). Построение проекции А₁ выполняется по линии связи, а проекции А₂ – перенесением координаты z_A из плоскости П₄ на плоскость П₂.

2. Построение точек В и С, расположенных на линиях фронтального очерка тора, осуществляется с помощью фронтальной плоскости b, параллельной плоскости П₂ и проходящей через ось вращения тора (см. вырожденную проекцию b₁ этой плоскости). Строим фронталь                  f ¢ = aÇb. При этом f ¢₂ çç f₂. Проекции В₂ и С₂ точек В и С находим в пресечении линии f ¢₂ с линиями фронтального очерка тора.

3. Построение промежуточных точек (например, точек 2, 2¢) можно осуществлять произвольным их выбором на плоскости П₄. Затем с помощью окружности (параллели) m строим горизонтальные проекции выбранных точек, а с помощью координаты z (см. отрезки, помеченные на чертеже тремя штрихами) строим фронтальные проекции этих точек.

4. Для соблюдения симметрии строимой фигуры сечения (особенно её фронтальной проекции) рекомендуется построить линию симметрии АК и точки В¢ и С¢, симметричные ранее найденным точкам В и С, относительно этой прямой (см. отрезки, помеченные на чертеже волнистыми линиями и крестиками).

5. Найденные проекции точек соединяем плавной кривой с учётом видимости линии сечения. Граница видимости лини сечения на плоскости П₂ определяется очерковыми точками В и С.

Задача 5. Построить точку К пересечения поверхности Ф с линией l.

Алгоритм решения в общем случае (рис. 92):

1. Через линию l проводим вспомогательную поверхность S.

2. Строим линию m пересечения поверхностей Ф и S:
        m = Ф Ç S.

3. Определяем искомую точку: К = l Ç m.

В общем случае точка К может быть не единственной.

Рассмотрим частные случаи этой задачи, когда линия l является прямой линией. Тогда в качестве поверхности - посредника S  может быть использована плоскость a.

  На рис. 93 показано применение фронтальной плоскости a для построения точек М и N пересечения тора Ф с прямой l.

На рис. 94 показан рациональный способ применения плоскости a общего положения, проходящей через прямую l и вершину S конуса. Тогда сечение конуса произойдёт по простейшей фигуре - D SAB. Алгоритм решения задачи:

1. Через произвольную точку К, расположенную на  прямой l, и вершину S конуса проводим прямую m. Тогда прямыми l и m определяется вспомогательная плоскость a (l Ç m).

2. Строим точки Q и T пересечения прямых l и m с плоскостью основания конуса.

3. Находим точки А и В пересечения линии QT с окружностью основания конуса и соединяем их с вершиной S конуса. Получаем фигуру сечения - D SAB.

Находим точки M, N = l Ç SAB.

Аналогичное решение показано на рис. 95. Здесь вспомогательная плоскость a проведена через прямую l, параллельно образующим цилиндра. Для этого через произвольную точку К, лежащую на заданной прямой l, проводим линию m, параллельно образующим цилиндра В этом случае рассечение цилиндра произойдёт по параллелограмму ABCD, который строим по точкам Q и T пересечения прямых l и m с плоскостью нижнего (или верхнего) основания цилиндра.

Иногда для получения рационального решения задачи по определению точек пересечения кривой поверхности с прямой линией используется преобразование чертежа.

На рис. 96 показано применение метода замены плоскости проекций П₂ на П₄, в результате чего построены новая проекция l₄ прямой l и неискажённая проекция с₄ окружности с – фигуры сечения сферы вспомогательной плоскостью a. Далее найдены проекции А₄ и В₄ искомых точек пересечения сферы с прямой l (А₄, В₄  = с₄ Ç l₄) и по линиям связи построены проекции этих точек в исходной системе плоскостей проекций.

 На рис. 97 показано применение метода замены плоскости проекций П₁ на П₄ для определения точек А и В пересечения цилиндра вращения с прямой l. Здесь ось х₂₄ новой системы

плоскостей проекций расположена перпендикулярно оси вращения цилиндра. В результате чего цилиндр отобразился на плоскость П₄ вырожденно – в виде окружности и там легко определяются искомые точки.

На рис. 98 показано использование метода вращения для нахождения точек А и В пересечения тора с прямой l. Указанный вариант преобразования возможен, если прямая l пересекается с осью i вращения поверхности. После поворота прямой l относительно оси i до положения, когда прямая окажется в плоскости a главного меридиана поверхности тора, легко определяются фронтальные проекции  искомых точек пересечения сначала в повёрнутом положении (А ₂ и В ₂), а затем и в исходном положении (А₂ и В₂).

На рис. 99 показан пример построения точек пересечения тора и окружности. Алгоритм построения:

1. Через точку О¢ - центр заданной окружности с проводим перпендикуляр к плоскости этой окружности и находим точку О пересечения этой прямой с осью i вращения тора.

2. Из найденной точки О как из центра строим сферу радиуса R _С, проходящую через окружность с.

3. Строим окружность m – линию пересечения тора и сферы.

4. Находим точки  А и В пересечения двух окружностей (А, В = с Ç m). Найденные точки и будут решением поставленной задачи.

Задача 6. Построить линию m пересечения двух поверхностей Ф и W.

Алгоритм решения задачи в общем случае (рис. 100):

1. Строим вспомогательную поверхность S. Выбор формы и положения этой поверхности в пространстве обусловлен необходимостью рассечения ею двух заданных поверхностей Ф и W по простейшим линиям каркаса.

2. Строим линию (линии) каркаса поверхности Ф:
q, q ¢ = Ф Ç S.

3. Строим линию каркаса поверхности W:   t = W Ç S.

4. Определяем точки, принадлежащие искомой линии m: 1, 2,… = q, q¢ Ç t.

5. Изменяем положение или размеры поверхности S (S¢), и повторяем пункты 2¸4 алгоритма до тех пор, пока не построим необходимое число точек (не менее восьми точек).

6. Соединяем построенные проекции точек лекальными кривыми с учётом видимости
линии m. Границами видимости линии m являются точки, расположенные на очерке той поверхности, которая располагается ближе к наблюдателю. Указанные очерковые точки должны быть предварительно построены.

В зависимости от вида  вспомогательной поверхности S различают два метода построения линии пересечения кривых поверхностей:

1. Плоских сечений, когда поверхность S является плоскостью.

2. Секущих сфер, когда поверхность S является сферой.

Метод плоских сечений. Этот метод применяют, если две пересекающиеся поверхности можно рассечь плоскостью – посредником по простейшим линиям каркаса (рис. 101).

На рис.102 показано построение линии m пересечения конуса вращения Ф и сферы W  с применением горизонтальных плоскостей – посредников a. Сначала определяем граничные уровни возможных сечений. Для этого в общей плоскости симметрии g находим экстремальные точки: точку А, имеющую аппликату z_max и точку В (z _min). Верхний предельный уровень рассечения должен располагаться ниже точки А, а нижний предельный уровень рассечения должен проходить выше точки В. В каждом уровне рассечения строим две окружности: q на сфере и t на конусе. Находим точки 1 и 2 их пересечений (сначала на плоскости П₁, а затем по линии связи на П₂). На фронтальную плоскость  проекций линии пересечения поверхностей проецируется параболой (линия m₂). Границами видимости горизонтальной проекции m₁  являются точки С и D, расположенные на экваторе сферы. Эти точки определяем рассечением плоскостью a¢.

На рис. 103 показан пример построения линии пересечения конуса и цилиндра вращения, оси которых являются скрещивающимися прямыми. Для решения задачи можно применять горизонтальные плоскости-посредники, рассекающие цилиндр по двум образующим, а конус - по окружности. Точки пересечения указанных линий определят точки, принадлежащие линии пересечения этих поверхностей.

Однако можно идти и другим путём. Проекция цилиндра на П₂ в виде окружности является вырожденной. На ней располагаются фронтальные проекции всех точек цилиндрической поверхности, включая точки, принадлежащие линии m пересечения рассматриваемых поверхностей. Следовательно, задача сводится к построению по заданной проекции m₂   линии m, расположенной на поверхности конуса,ее недостающей проекции m₁. Она решается каркасным способом. См., например, построение точек 1 и 2 с помощью окружности t на конусе. Границами видимости линии m на плоскости П₁  являются точки С и D, расположенные на горизонтальной очерковой образующей цилиндра.

Метод вспомогательных сфер имеет две разновидности: метод концентрических и метод эксцентрических сфер.

1. Метод концентрических сфер применяется для построения линии пересечения двух поверхностей вращения, оси которых пересекаются и образуют общую плоскость симметрии, параллельную одной из плоскостей проекций. Метод сфер использует следующее свойство: две соосные поверхности вращения пересекаются между собой по окружностям – общим параллелям. Соосными называются поверхности вращения, оси которых совпадают.

Рассмотрим сначала взаимодействие двух соосных поверхностей вращения, одна из которых является сферой. На рис. 104. показана фронтальная проекция Ф₂ конуса вращения и двух соосных с ним сфер: сферы S, вписанной в конус и сферы S ¹, пересекающейся с конусом. В первом случае сфера S и конус Ф касаются друг друга по окружности q, а во втором случае пересекаются между собой по двум окружностям q ¢и q ². При этом плоскости указанных окружностей перпендикулярны оси i конуса. На рис. 105 показано взаимодействие цилиндра вращения W с соосными с ним сферами. Это взаимодействие осуществляется по окружности   t касания для сферы S, вписанной в цилиндр, и по двум окружностям  t ¢ и t ² для сферы S ¹, пересекающей цилиндр. Плоскости указанных окружностей перпендикулярны оси j цилиндра.

На рис. 106. показано применения метода концентрических сфер для построения линии пересечения конуса и цилиндра. Алгоритм построения:

1. Находим точку пересечения осей: О = i Ç j и общую плоскость симметрии g (i Ç j) çç П₂.

2. Строим сферу минимального радиуса, вписанную в одну из поверхностей (в нашем случае в конус) и пересекающую другую поверхность (цилиндр).

Радиус сферы R _min  можно определить как наибольшую длину одного из двух перпендикуляров ОК или ОТ, построенных из точки О к очерковым образующим конуса и цилиндра (рис. 106, а).

3. Строим окружность q касания конуса и сферы R _min  (Рис. 106, б)

4. Строим две окружности t и t¢ пересечения цилиндра и сферы R _min  

5. Строим точки: 1 (1¢), 2 (2¢) = q Ç t, t¢, принадлежащие линии пересечения конуса и цилиндра.

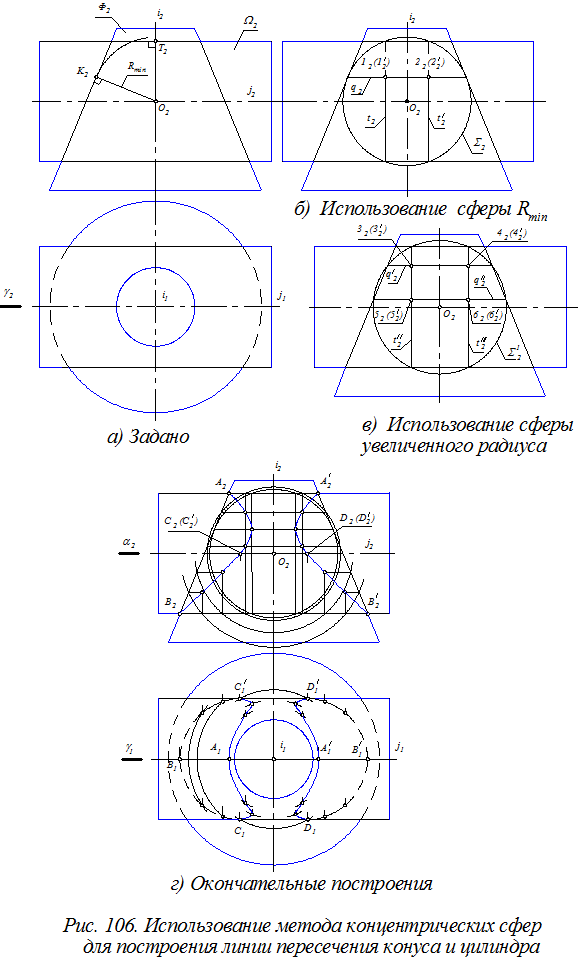
6. Увеличиваем радиус сферы (рис. 106, в).

7. Строим две окружности  q ¢ и q ²   пересечения конуса и новой сферы.

8. Строим две окружности t ² и t ¢² пересечения цилиндра и новой сферы.

9. Строим точки: 3 (3¢), 4 (4¢), … = q ¢ ,q ¢¢Ç t ¢¢, t ¢¢¢, принадлежащие линии пересечения конуса и цилиндра.

10. Повторяем пункты 6¸9 алгоритма до получения необходимого количества точек, принадлежащих линии пересечения (рис. 106, г). Максимально возможный радиус вспомогательной сферы определяется расстоянием от точки О до наиболее удаленной точки пересечения линий фронтальных очерков исходных поверхностей (точки В или В ¢).

11. Построение горизонтальных проекций линий пересечения осуществляется с помощью окружностей каркаса конуса. При этом  необходимо определить точки С (С ¢) и D (D ¢), расположенные на линиях горизонтального очерка цилиндра, т. к. эти точки являются границами видимости линий пересечения на плоскости П₁. Определение горизонтальных проекций указанных точек осуществляется построением окружности на конусе, лежащей в горизонтальной плоскости a. Эта плоскость проходит через ось цилиндра и рассекает эту поверхность по очерковым образующим.