2020-05-21
1165
Запишем уравнение Эйнштейна для фотоэффекта (4.19) в следующем виде:
.
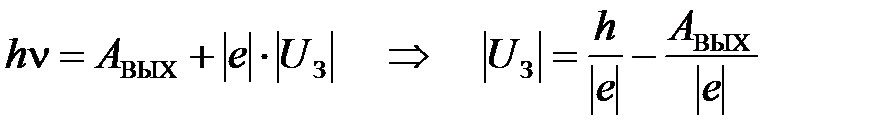График этой зависимости приведен на рис. 4.4. По графику можно найти постоянную Планка h (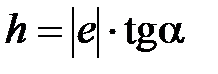
) и красную границу 
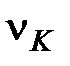для данного металла (по точке пересечения графика с осью частот: 
).
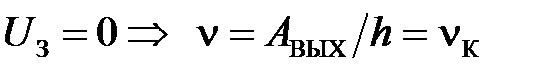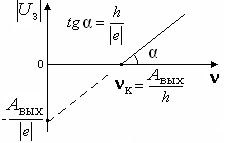
Рис. 4.4
Эффект Комптона
Рассмотрим эксперимент по рассеянию рентгеновского излучения веществом. Пучок рентгеновских лучей с определенной длиной волны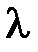 
падает на кристалл и рассеивается им под разными углами (рис. 4.5, а).
В рассеянном излучении наряду с излучением длиной волны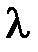 
(несмещенная компонента излучения) появляется излучение с длиной волны 
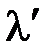(смещенная компонента излучения), причем 
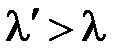(рис. 4.5, б) [4].
Эффект Комптона заключается в появлении смещенной компоненты в рассеянном веществом рентгеновском излучении. Причем, длина волны смещенной компоненты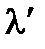 
не зависит от природы рассеивающего вещества и рассчитывается по формуле
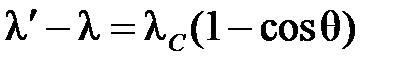, (4.24)
где величина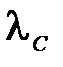 
называется комптоновской длиной волны. Она равна
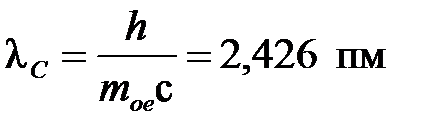, (4.25)
где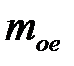 
– масса покоя электрона.
В рассмотренном ранее явлении фотоэффекта, при облучении металла излучением видимого диапазона, энергия падающего фотона мала по сравнению с энергией покоя свободного электрона (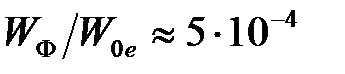
), поэтому происходит поглощение фотона электроном [4].
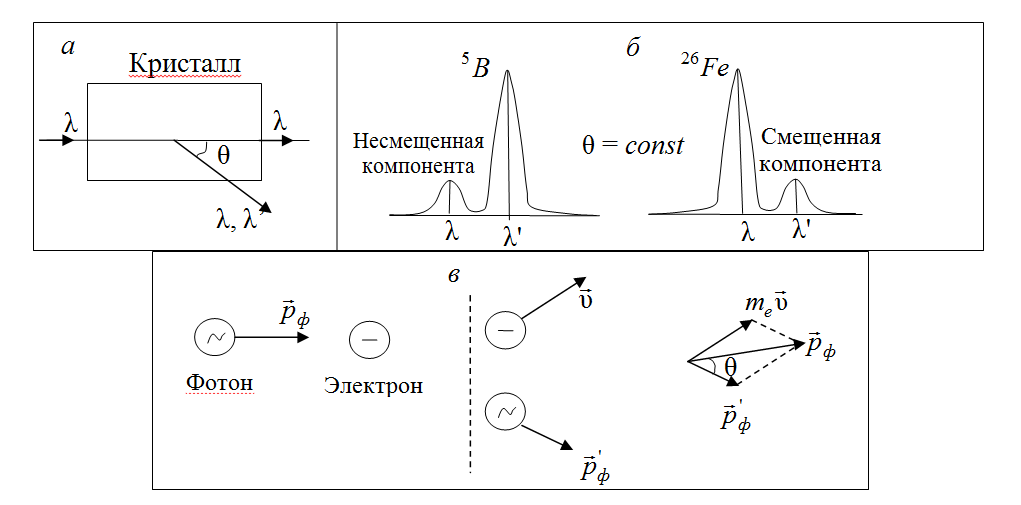
Рис. 4.5
В области рентгеновских лучей энергия фотона возрастает настолько (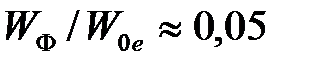
), что при взаимодействии фотона со свободным электроном (его энергия связи с атомом значительно меньше энергии налетающего фотона), происходит процесс упругого рассеяния фотона на электроне. При этом возникает смещенная компонента излучения.
При выводе формулы (4.24) использованы законы сохранения энергии (4.26) и импульса (4.27) для процесса упругого взаимодействия электрона и фотона (рис. 4.5, в)
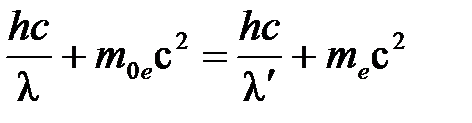, (4.26)
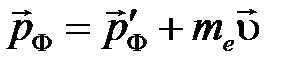. (4.27)
Несмещенная компонента возникает при рассеянии фотонов на сильно связанных с атомами электронах, для них энергия связи с атомом значительно превосходит энергию налетающего фотона [4]. Поэтому процесс рассеяния фотона будет происходить не с электроном, а с атомом, что приводит к существенному уменьшению различия между длинами волн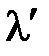 
и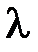 
(данное различие в эффекте Комптона вообще не обнаруживается).
Для атомов с малым атомным номером преобладают электроны, слабо связанные с атомами. Поэтому для таких элементов в основном наблюдается рассеяние фотонов на свободных электронах. Следовательно, для элементов с малыми номерами в таблице Менделеева, интенсивность смещенной компоненты 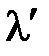будет больше интенсивности несмещенной компоненты 
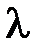(рис. 4.5, б). Для атомов с большими атомными номерами будет преобладать число электронов, сильно связанных с атомами, поэтому интенсивность несмещенной компоненты будет больше (рис. 4.5, б) [4].
