Задача для самостоятельного решения

ПЛАН

1. Основные понятия

2. Математическое моделирование при решении задач

3. Задача для самостоятельного решения

Основные понятия

Модель – это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала

Моделирование – исследование объектов познания на их моделях, построение и изучение моделей реально существующих предметов, процессов или явлений с целью получения объяснений этих явлений, а также для их предсказания.

Разновидности моделей. Модели принято делить на два класса: физические и математические. Физические модели имеют ту же физическую природу, что и оригинал. Физической моделью является, например, аэродинамическая труба, в которой устанавливается самолёт для исследования поведения его органов управления при продувании трубы воздухом с такой же скоростью, как при реальном полёте. Физическим моделированием являются испытания опытных образцов различной аппаратуры на тряску, давление и т.д. Математическая модель – это точное или приближённое математическое описание свойств или закономерностей функционирования оригинала.

Определение 1. Математическая модель – это «эквивалент объекта, отражающий в математической форме важнейшие его свойства – законы, которым он подчиняется, связи, присущие составляющим его частям». «Математическое моделирование – процесс построения и изучения математических моделей реальных процессов и явлений».

Определение 2. Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе.

Определение 3. Математическая модель – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная задача математического моделирования – не только исследовать эти объекты, но и предсказать результаты будущих наблюдений.

Математическое моделирование при решении задач

Очень часто при решении практической задачи удается, изучив условие задачи, построить её математическую модель, на этой модели осуществить решение задачи, а затем перевести результат решения на язык исходной ситуации, т.е. сделать практический вывод. В этом и состоит могущество математического метода познания природы, широкая прикладная направленность математики.

В науке широко используется метод моделирования и заключается он в том, что для исследования какого-либо явления или объекта, выбирают или строят другой объект, в каком-то отношении подобный исследуемому объекту. Построенный или выбранный объект изучают и с его помощью решают исследовательские задачи, а затем результаты решения этих переносят на первоначальное явление или объект.

Например, разрезая конус плоскостями, получаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы. Математики еще в древности начали изучение этих кривых, результаты которых имеют большое значение для физики, техники, астрономии, военного дела, где очень часто встречаются эти кривые. Однако лишь тогда, когда, пользуясь методом Декарта и Ферма, были составлены уравнения этих кривых, их изучение сразу резко продвинулось вперед и с помощью этих уравнений - моделей кривых конических сечений: были решены все основные задачи, с ними связанные. Заметим, что уравнения кривых выступают в качестве моделей соответственно окружности, эллипса, параболы и гиперболы, а эти кривые в свою очередь можно рассматривать как геометрические модели данных уравнений.

Задача № 1.

Для размещения склада требуется огородить участок прямоугольной формы наибольшей площади имеющейся для этого сеткой длиной 80 м. Найдите длину и ширину участка.

Решение: обозначим длину одной из сторон искомого прямоугольника через х м, тогда площадь S (х) прямоугольника выразится формулой: S (х) = х(40 - х)=40х - х 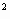, где х 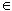(0; 40).

Исследуя полученную функцию на max и min, находим критические точки: S’ (х) = 40 – 2x, 40-2х = 0 => x = 20

убеждаемся, что участок наибольшей формы - квадрат 20х20 м, max S(x)=400 м².

Сделаем процесс моделирования для этой задачи динамичным. Для этого вводим дополнительные условия, соответствующие реальной ситуации, например, в таком виде: "Как правило, склад строится не на открытом месте, а около каких-либо построек. Какие возможны случаи ограждения склада?"

Наиболее часто встречаются два случая:

1) когда склад примыкает к одной стене постройки;

2) одновременно к двум стенам постройки.

В первом случае, видим, что площадь S(x) выражается уже другой формулой S(x) = 2x(40 - x), где х м - длина стороны, не примыкающей к постройке. Исследуя эту функцию, приходим к выводу, что в этом случае оптимальные размеры таковы: длина стороны, примыкающей к постройке 40 м, длина другой стороны 20 м, наибольшая площадь равна 800 м².

Во втором случае видим, что S (x)= x(80 - x). Исследуем функцию S (x)= 80 x – x².

S’ (x)= 80 – 2x. Одна критическая точка х = 40. Искомая площадь S (40) =1600 (м²).

Итак, одна из характерных особенностей математического моделирования состоит в сопоставлении построенной модели с описываемым ей явлением. Результатом такого сопоставления, как правило, является учет каких-то новых моментов в рассматриваемом явлении, следовательно, и уточнение модели.

Задача № 2.

При движении теплохода по озеру расходы N в рублях на 1 км пути определяется по формуле N(v)=аv 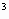+ 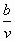, где v - скорость теплохода (в км/ч), a и b - определяемые из опыта коэффициенты. Найдите скорость теплохода, при которой расходы будут наименьшими, если, а = 0,001 и b=60.

Решение: с помощью производной находим значение скорости v, при которой функция N(v) = 0,001v 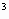+ 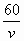достигает наименьшего значения на интервале (0;+ 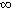): v=12 км/ч, min N(v) = N(12) 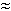6,728 (рубля на 1км).

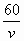Затем рассматривается ситуация, при которой, согласно маршруту, движение теплохода продолжается по реке против течения. Опытным путем установлено, что при таком движении расходы увеличиваются на величину,

пропорциональную скорости движения, т.е. N(v) = 0,001v 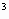+   + kv, где k - коэффициент пропорциональности.

Чтобы определить значение коэффициента k, необходимо использовать какие-либо начальные условия. Например, известно, что при скорости в 20 км/ч расходы N(20) = 12,2 рубля на 1 км.

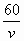Формулируется задание: "Найдите значение k и определите скорость теплохода по реке против течения, при которой расходы N минимальны". Подставляем начальные условия и получаем значение коэффициента k =0.06, уточняется математическая модель- функция N:

N(v) = 0001v 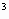+ + 0,06v, описывающая расходы при движении

теплохода,определяется наивыгоднейшее значение скорости v:                      v 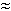11,4 км/ч, при этом min N(v) = N(11,4) 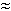7,4 (рубля на 1 км пути).

В пищевой, химической и других отраслях промышленности в огромных масштабах используются металлические сосуды, имеющие форму прямоугольного параллелепипеда. По технологическим соображениям эти сосуды изготовляются с заданным отношением высоты k сосуда к одному из размеров основания. В целях экономии требуется, чтобы при изготовлении сосудов заданной ёмкости расход металла, эмалей, лаков, красок, широко применяющихся в качестве покрытий, был возможно меньшим.

Важное практическое значение приобретает такая задача:

Задача № 3.

Каковы должны быть размеры прямоугольного сосуда заданной ёмкости V с заданным значением величины k, чтобы расход металла на его изготовление был наименьшим?

Решение: если расход металла на швы не учитывать, а толщину стенок, дна и крышки считать одинаковой, то за параметр, определяющий расход металла на изготовление сосуда, принять площадь S его поверхности.

Обозначим размеры сосуда через x, y, z и пусть z=ky, то получим:

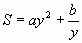, где a=2k, .

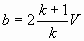Функция S имеет наименьшее значение при 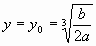и что решение задачи задаётся формулами

, , .

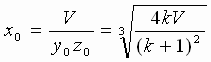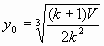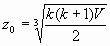Прямоугольные сосуды различной ёмкости производятся в стране в огромных количествах, то становится очевидным, что отступление от оптимальных размеров приводит к значительным убыткам.

Приведем условия задач и дополнительные задания к ним, позволяющие акцентировать внимание на динамическом характере математической модели, выработать первоначальные навыки уточнения модели. Такого рода упражнения могут быть использованы по усмотрению учителя при закреплении умений, связанных с решением задач одномерной оптимизации в домашних, самостоятельных, проверочных и других работах.

Задача для самостоятельного решения

Задача № 4.

Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200м, и площадь её при этом оказалась наибольшей. Каковы размеры площадки?