Тема «Неопределенный интеграл. Интегрирование по частям»

Группа 314.                                                          Дата 27.04.20

Урок 1

Тема:   Интегрирование методом замены переменной.        Интегрирование по частям.

Цели:

  научиться применять метод замены переменной при вычислении неопределенного и определенного интеграла.

Оснащение занятия: конспект лекций.

Тип: комбинированный.

Ход урока.

Орг. момент.

Порядок выполнения работы:

Задание 1.

- Ознакомиться с лекциями

 - Выписать тетрадь примеры на применение метода замены переменной при вычислении неопределенного интеграла.

Задание 2.

Решить примеры для самостоятельного решения.

 

Изучение нового материала.

 Неопределенный интеграл. Метод замены переменной.

В основе интегрирования методом замены переменной лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если ,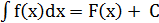

то                                       ,

где u(x) – произвольная дифференцируемая функция от х.

    Замена переменной в неопределенном интеграле производится с помощью подстановок следующих двух типов:

1) х =  (t), где t – новая переменная, а  (t) – непрерывно дифференцируемая функция. В этом случае формула замены переменной такова:

(1)

Функцию (t) стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный для интегрирования вид;

2) t = 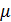(x), где t – новая переменная. В этом случае формула замены переменной имеет вид:

Примеры.

1.

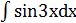
Решение. Данный интеграл окажется табличным, если под знаком дифференциала будет находиться аргумент 3х подынтегральной функции . Так как d(3x) = 3dx, то

 =

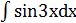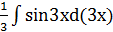
Следовательно, подстановка 3х = t приводит рассматриваемый интеграл к табличному: 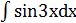 =  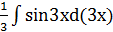=  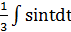= - cost + C

Возвращаясь к старой переменной х, окончательно получим

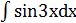 = - cos3х + C

2.

Решение. Так как d(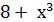) = 3х²dx, то

Полагая 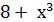 = t, получим

 + C =  + C.

3.

Решение. Поскольку d(sinx) = cosx, имеем

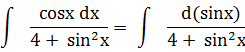
Поэтому, используя подстановку t = 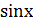, приходим к табличному интегралу:

 =  =  =

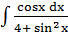4.

Из соотношения d(  получаем

 =

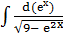
Воспользовавшись подстановкой t = , приходим к табличному интегралу:

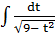 =  = arcsin

5.

Решение. Здесь используем подстановку 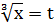. Отсюда х = t³, dx = 3t²dt и, следовательно по формуле (1) находим

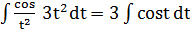 =  = 3sin t + C

Возвращаясь к старой переменной х, получим

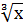 = 3sin  + C

6.

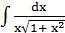
Применим подстановку x = . Тогда dx = - ,  = , t =

По формуле (1) находим

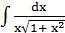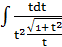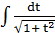 = -  = -  = - ln  + C

Возвращаясь к старой переменной х, получим

- ln  + C = - ln  + C = -ln  + x

Практическая часть.

Вычислите интегралы, используя метод замены переменной:

1.

2.

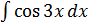
3.

4.

5.

6.

Учебник стр. 175 № 6.19(а, в, е), № 6.20 (а,в). № 6.73(а) стр. 196.

    4. Итог. Д/З.

№ 6.19 (б,г, д), №6.20 (б, г) стр. 175 учебника

№ 6.73 (б) стр. 196.

 

Урок 2.                Дата 28.04

Тема  «Неопределенный интеграл. Интегрирование по частям».

Цель:    научиться применять метод интегрирования по частямпри вычислении неопределенного и определенного интеграла.

    Тип: комбинированный.

Ход урока

Орг. момент.

Задание 1.

- Ознакомиться с лекциями

 - Выписать тетрадь примеры на применение метода интегрирования по частям при вычислении неопределенного интеграла.

Задание 2.

Решить примеры для самостоятельного решения.