2020-05-21
74
Интегрированием по частям называется нахождение интеграла по формуле 
(1)
где 
и 
- непрерывно дифференцируемые функции от х. С помощью формулы (1) отыскание интеграла 
сводится к нахождению другого интеграла 
, её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве берется функция, которая при дифференцировании упрощается, а в качестве 
- та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так при нахождении интегралов вида
за 
следует принять многочлен 
, а за - соответственно выражения 
, 
; при отыскании интегралов вида
за принимаются соответственно функции 
, а за - выражение 
.
Примеры.
1. 
. Положим 
= lnx, 
= 
, откуда
du = 
, v = 
Тогда по формуле (1) находим
= lnx(
= - 
+ 
= - - 
+ С
2. 
Решение. Полагая = 
= 
найдем du = 
,
v = 
= 
Следовательно,
= 
= 
3. 
Решение. Пусть = 
, 
= 
du = 
, v = 
По формуле (1) находим
= 
- 
(
К последнему интегралу снова применим формулу интегрирования по частям.
Положим = 
, = 
du = , v = и, следовательно, 
- 
= 
Подставляя найденное выражение в соотношение (, получим
= 
(
4. 
Положим = 
= 
, откуда du = 
, v = 
Используя формулу (1), находим
=
= 
- х + 
5. 
Решение. Пусть = 
; тогда du = - 
v = - 
Согласно формуле (1) имеем
I = = = - 
. (
К последнему интегралу снова применяем интегрирование по частям. Полагая = 
, находим du = - v = 
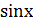и, следовательно, 
= 
Подставляя полученное выражение в соотношение (
приходим к уравнению с неизвестным интегралом I:
I = = - 
- 
– I,
Из которого находим
I = - 
(
Практическая часть.
Вычислите интегралы, используя метод интегрирования по частям:
1. 
2. 
3. 
4. 
5. 
Плюс учебник стр. 175 № 6.21(а, б), № 6.22(а,в).
5. Итог. Д/З.
№ 6.21(в,г), 6.22(б,г) стр. 175.
