Варианты ранжирования

Градация	Ранг	Альтернативный ранг 1	Альтернативный ранг 2
Согласен	1	5	1
Скорее согласен, чем не согласен	2	4	3
Не уверен	3	3	5
Скорее не согласен, чем согласен	4	2	7
Не согласен	5	1	9

 

Как видно из таблицы, альтернативные ранги, несмотря на различие в числовом представлении, сохраняют свою последовательность (возрастания или убывания), что говорит о верности приписывания рангов. Для проверки правильности ранжирования применяют также формулы:

,

(1)

где N – число ранжируемых признаков.

В случае, если количество ранжируемых признаков велико, формула (1) может быть модифицирована:

,

(2)

где X – число строк,

Y – число столбцов.

Зачастую при ранжировании признаков может возникнуть ситуация одинаковых рангов, т. е. несколько величин могут иметь сходные числовые обозначения. В этом случае ранжирование производится следующим образом:

1. Выявляются наименьшее и наибольшее значение числового ряда.

2. Наименьшему значению присваивается ранг, равный 1, наибольшему – равный количеству ранжируемых величин.

3. В случае совпадений рангов величин они ранжируются последовательно таким образом, чтобы каждая из них имела ранг, превышающий предыдущий на единицу ранжирования.

Для проверки правильности ранжирования проводится расчет по формулам (1) или (2).

Допустимыми методами статистики являются медиана, проценты, ранговая корреляция по Спирмену, Кендаллу.

3. Интервальная шкала.

В основе шкалы лежит понятие интервала – части измеряемого свойства между позициями шкалы. Измерение заключается в присвоении измеряемому свойству определенного значения, равного количеству единиц измерения, соответствующих имеющемуся свойству. Размер интервала – фиксированная величина, постоянная для всех участков шкалы. Важной особенностью шкалы интервалов является отсутствие нуля – единой точки отсчета. Для использования шкалы интервалов нередко применяют специальные единицы измерения – стэны, станайны. Из табл. 6 видно, что приведенная шкала интервалов имеет семиуровневую градацию трех вариантов утверждения, доступных испытуемому.

Таблица 6

Шкала интервалов

	–3	–2	–1	0	+1	+2	+3
	Не согласен		Не уверен			Согласен

Классическим примером измерения в шкале интервалов является методика «Семантический дифференциал» Ч. Осгуда, где испытуемый сопоставляет субъективные представления с заранее определенной шкалой интервалов, тем самым определяя их выраженность.

4. Шкала отношений.

В отличие от шкалы интервалов в шкале отношений вводится фиксированная точка отсчета, т. е. понятие ноля. В связи с этим измерение в шкале отношений предполагает сопоставление объектов в зависимости от степени выраженности измеряемого свойства. Шкала отношений используется в естественно-научном измерении (вес, объем, протяженность, сила и пр.). Данная шкала обладает максимальной мощностью,т. е.способностью дифференцировать большинство признаков или свойств психического явления, в отличие от номинативной, порядковой или интервальной.

Распределение

В результате измерения накапливается совокупность значений свойства, выраженных в определенной шкале. Закономерность, с которой данные значения представлены на всем пространстве шкалы, называется распределением[14]. В работах Ф. Гальтона впервые было установлено, что психологические явления подчиняются закону нормальности распределения, т. е. могут быть описаны формулой:

 

,

(3)

где М_х (математическое ожидание) и σ ²_х (дисперсия) – параметры распределения;

λ_х – интервал группировки данных (отличный от единицы);

π  = 3,14…;

е = 2,17.

Данная формула претерпела множество изменений, прежде чем утвердилась в своем окончательном виде в психологии. П. Лаплас сформулировал функцию симметричного распределения интегральных вероятностей, послужившего фундаментом для работ Ф. Гаусса, открывшего закон распределения вероятностей – закон нормального распределения, что было подтверждено работами А. Кеттле. Кеттле указывал, что средняя величина встречается в совокупности измерений чаще, чем отклоняющаяся от среднего. Причем чем больше это отклонение, тем реже данная величина встречается. Графически это показано на рис. 1. Интервал М ± σ описывает площадь под кривой, в которую входит 68,3 % проявлений психического явления. Интервал М ± 2σ – 95,4 %, а интервал М ± 3σ соответствует 99,7 % площади. Таким образом, кривая нормального распределения описывает частоту интенсивности изучаемого психического явления и представляет собой графическое выражение формулы (3). Важное следствие закона о нормальности распределения – возможность стандартизации измерений, т. е. графически, приведения их к некоей стандартной, эталонной кривой. Так как результаты любого измерения могут быть выражены через М – среднее и σ – стандартное отклонение, то возникает возможность стандартизации измерения согласно формуле (4):

 

,

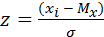(4)

где Z = стандартизованное значение;

х_i – значение переменой, значение среднего для х.

Полученное распределение характеризуется следующими свойствами:

– среднее (М) для такого распределения = 0, σ = 1;

– кривая приближается к оси z асимптоматически;

– кривая симметрична при М = 0, ее асимметрия и эксцесс равны 0;

– площадь между кривой и осью z равна 1.

Алгоритм приведения к нормальному виду, по О. А. Попову, выглядит следующим образом, учитывая, что при нормальном распределении в интервал m ± 1σ попадает 68,26 % всей выборки, этот интервал и принимается за средние баллы. Все значения до него относятся к низким, а выше него – к высоким. Таким образом, получаем три градации баллов. Для подобной стандартизации можно использовать интервал m ± ²/₃σ, тогда 50 % выборки попадает в средние и по 25 % – в низкие и высокие баллы. Каким будет интервал – выбирает сам исследователь. Разделение на 4 интервала осуществляется подобным образом, граница между вторым и третьим интервалом проходит по среднему арифметическому.

Разделение на пять уровней применяется при сильном разбросе данных. В подобном случае добавляется интервал m ± 2σ.

Недостатком «уровневой» стандартизации является то, что полученные уровни с трудом поддаются последующей статистической обработке и слишком малоинформативны.

Применение закона нормальности распределения – важный этап при проведении математико-статистической обработки эмпирических данных.

Рис. 1. Кривая нормального распределения

М – среднее значение, σ – стандартное отклонение,
ƒ – частота выраженности признака

Именно характер распределения определяет стратегию дальнейшего анализа данных. Так, если эмпирическое распределение соответствует нормальному, возникает возможность применения параметрических методов статистического анализа. В обратном случае используются непараметрические методы. Причины несоответствия полученного распределения нормальному могут заключаться как в объективной природе регистрируемого явления, так и в самой процедуре измерения.

Вопрос о нормальности распределения значений психических явлений актуален на протяжении всего периода применения математических методов в психологии. К примеру, И. Кант отрицал возможность применения статистического анализа для изучения психических явлений, утверждая, что человеческая душа метафизична и не может подлежать формальному исследованию. Противники этой точки зрения утверждают, в свою очередь, что без эксперимента, процедуры измерения психология не может являться подлинно научной дисциплиной. Процедура исследования, в свою очередь, влияет на нормальность распределения, к примеру, в связи с неравномерной «чувствительностью» инструментария. Таким образом, при изучении умственных способностей путем решения задач, ряд из них может быть неразрешим или, наоборот, чрезвычайно прост для испытуемых. В подобном случае на графике распределения будет отражена асимметрия (смещение) линии графа от среднего в сторону меньших или больших значений. Показатель эксцесса (плосковершинности или остроты) графика распределения свидетельствует о преобладании определенного частотного диапазона значений изучаемого явления по выборке.

Проверка полученного распределения на нормальность базируется на вычислении ряда дескриптивных статистик.

Дескриптивная (описательная) статистика – это различные статистические показатели, описывающие распределение данных. К ним относятся среднее, мода, медиана, разброс, дисперсия и стандартное отклонение.

Среднее (арифметическое):

,

(5)

где х_i – значение изучаемого явления (i указывает на порядковый номер зафиксированного значения);

n – количество наблюдений.

Мода (Мо) – наиболее часто встречающееся значение признака в выборке. Мо вычисляется определением частоты ƒ встречаемости признака. В случае если несколько близких членов ряда обладают одинаковой частотой встречаемости, то Мо выборки определяется их среднеарифметическим значением. В выборке могут существовать несколько мод, в данном случае выборка является бимодальной, или есть возможность выделения генеральной моды и нескольких локальных.

Медиана (Md) – значение признака, разделяющее выборку на две симметричные части. Md определяется путем ранжирования значений по выборке. В случае, если количество значений нечетное, то медиана – центральное (симметричное) значение, в противном случае медиана – среднее арифметическое нескольких центральных значений.

Разброс (R) определяет разброс значений по выборке от максимального к минимальному. Разброс вычисляется вычитанием из максимального значения минимального.

Дисперсия – мера рассеивания значений изучаемого явления (признака), характеризующая степень разобщенности измеряемых значений вокруг среднего.

,

(6)

где n – количество измерений;

Х – среднее арифметическое, вычисляемое по формуле (5).

Стандартное отклонение (σ) – среднее квадратическое отклонение, вычисляемое путем выделения квадратного корня из дисперсии:

(7)

Вычисление среднеквадратического отклонения – важный этап проверки предположения о нормальности распределения, принятия решения о выборе метода последующей статистической обработки данных.

Коэффициент вариации (V) есть отношение стандартного отклонения к среднему арифметическому значению, выраженное в процентах:

100 %, (8)

где s – среднеквадратическое отклонение;

 Х – среднее арифметическое вариативного ряда.

Коэффициент вариации используется для характеристики однородности исследуемой совокупности. Статистическая совокупность считается количественно однородной, если коэффициент вариации не превышает 33 % [15].

Исследование формы распределения. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т. е. оценку симметричности и эксцесса.

В статистике различают одновершинные и многовершинные виды кривых распределения. Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки[16].

Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.

Распределение называется симметричным, если частоты любых 2 вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях x = Mo = Me.

Асимметрия – показатель, отражающий перекос распределения относительно среднего арифметического влево или вправо. В тех случаях, когда какие-нибудь причины влияют на появление значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения[17].

На графике распределения, таким образом, будет отражена асимметрия (смещение) линии графа от среднего в сторону меньших или больших значений. Положительно асимметричным считается распределение с более крутым левым и более пологим правым крылом, распределение с отрицательной асимметрией, напротив, имеет более пологий левый фронт нарастания и более крутой правый (см. рис. 2).

Отрицательная  асимметрия,  As < 0	Симметричное  распределение,  As = 0	Положительная  асимметрия,  As > 0

Рис. 2 Типы асимметрии

Рассчитываемый по соответствующим формулам коэффициент асимметрии (As) может быть использован в качестве одного из критериев соответствия экспериментального распределения теоретическому.

Вычисление коэффициента асимметрии:

Коэффициент асимметрии вычисляется по следующей формуле:

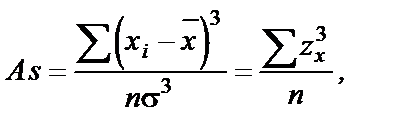   (9)

 

 где z_x – мера Пирсона .

 

 

При больших выборках (n > 50) можно использовать упрощенную формулу:

(10)

Соответствие эмпирического распределения нормальному находится по соответствующим таблицам. При этом эмпирическое распределение считается соответствующим теоретическому (нормальному), если асимметрия при данной выборке не превышает граничного значения.

Причины асимметрии могут быть различными.

Во-первых, это возможное действие побочных однонаправленных факторов. Так, например, в тестах на измерение интеллекта могут преобладать сложные задания, с которыми большинство испытуемых не справляется. Это может явиться причиной положительной асимметрии (центральная тенденция лежит слева от среднего значения).

Во-вторых, это ограничение (сверху или снизу) размаха вариаций. Например, при измерении времени сенсомоторной реакции нижний предел реагирования лимитирован физиологическими возможностями субъекта, в то время как верхний жестко не ограничен.

Наконец, третьей причиной асимметрии может быть неоднородность выборки (например, если исследование проводится в смешанной группе разного возраста). При этом имеет место наложение друг на друга двух или нескольких разных по численности и сдвинутых относительно друг друга по моде распределений.

Показатель эксцесса (плосковершинности или остроты) графика распределения свидетельствует о преобладании определенного частотного диапазона значений изучаемого явления по выборке.

В отличие от коэффициента асимметрии, коэффициент (показатель) эксцесса характеризует компактность или «размытость» распределения, его островершинность или плосковершинность, что связано с разным характером группирования значений переменной вокруг среднего (рис. 3).

 

Плосковершинное распределение, Ex < 0	Нормальное  распределение,  Ex = 0	Островершинное  распределение,  Ex > 0

Рис. 3. Типы эксцесса

Причинами эксцесса могут быть большая или меньшая степень тяготения переменных к центральной тенденции, неоднородность выборки, наложение друг на друга нескольких распределений с одинаковой модой и разной дисперсией и т. д. Вычисление показателя эксцесса:

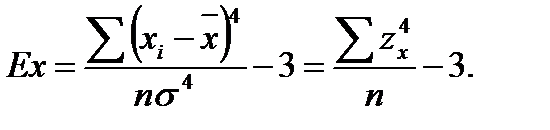        (11)

Теоретически величина эксцесса может варьироваться от – 3 до + ¥. Критерий согласия с нормальным распределением аналогично коэффициенту асимметрии определяется по таблицам граничных значений.

Аналогично определению асимметрии распределение соответствует нормальному (согласуется с нормальным), если Ex < Exкр. При обратном соотношении принято говорить, что по показателю эксцесса эмпирическое распределение статистически достоверно отличается от нормального.

При анализе эмпирического распределения может возникнуть такая ситуация, когда по одному из показателей (асимметрии или эксцессу) распределение соответствует нормальному, по другому же – отличается от него. В этом случае следует использовать следующее правило: если хотя бы по одному из вышеуказанных показателей распределение достоверно отличается от нормального, то следует делать вывод о том, что экспериментальное распределение отличается от теоретического (нормального).

Кроме коэффициента асимметрии и показателя эксцесса, для сравнения экспериментального распределения с теоретическим используют и другие критерии, в частности критерий хи-квадрат и критерий l Колмогорова – Смирнова.

Вычисление дескриптивных показателей – важный этап математико-статистического анализа, позволяющий с минимальными временными затратами дать общую описательную характеристику особенностей проявления изучаемого показателя в выборке.