Непараметрические процедуры математико-статистического анализа

В качестве непараметрического метода изучения корреляционных связей в выборке можно применять коэффициент ранговой корреляции Спирмена. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые представлены в виде рангов сравниваемых величин. Величина данного коэффициента ранговой корреляции лежит в интервале от –1 до +1. Как и линейный коэффициент Пирсона, может принимать положительные и отрицательные значения, характеризуя, в то же время, направленность связи между признаками, представленными в ранговой шкале.

Расчет коэффициента ранговой корреляции предполагает соблюдение ряда требований:

1. Сравниваемые переменные должны быть представлены в ранговой шкале.

2. Число сопоставляемых признаков должно быть одинаковым.

Формула расчета коэффициента корреляции по Спирмену при отсутствии в выборке одинаковых рангов выглядит следующим образом:

(18)

где

n – объем выборки (количество ранжируемых признаков);

D – разность между рангами по двум переменным для каждого испытуемого;

∑(D²) – сумма квадратов разностей рангов.

В случае если в выборке находятся одинаковые ранги, в формулу вычисления коэффициентов корреляции добавляются поправки на одинаковые ранги. Изменения претерпевает числитель формулы (18). В случае, если в первой сопоставляемой группе присутствуют одинаковые ранги, в числитель необходимо добавить следующий коэффициент (D1):

(19)

где n – число одинаковых рангов.

Таким образом, формула (18) модифицируется до:

(20)

После вычисления эмпирического значения ρ полученный коэффициент сопоставляется с табличным. Отметим, что табличные значения при расчете коэффициента ранговой корреляции Стьюдента от n = 5 до n = 40 представлены в табл. III прил. 2, при n > 40 справедливы критические значения коэффициента линейной корреляции по Пирсону (табл. IV прил. 2).

Критерий хи-квадрат (х²) распределения используется для расчета согласия эмпирического распределения теоретическому, а также для расчета однородности экспериментальных выборок. При совпадении эмпирического и теоретического распределения величина х²_ЭМП = 0, с увеличением этих значений расхождение также увеличивается.

Формула х²:

(21)

где

f_Э = эмпирическая частота;

f_m = теоретическая частота;

k = количество разрядов признака.

Для сравнения двух эмпирических распределений (в зависимости от вида представленных данных) формула для расчета х² распределения может иметь вид:

(22)

где N и M – количество элементов в сопоставляемых выборках.

Для расчета уровня значимости х² распределения используется понятие степени свободы, которое рассчитывается по формуле: v = k – 1, где k – количество элементов в выборке. Таблица критических значений приведена в табл. IV прил. 2.

Непараметрическим критерием, предназначенным для сравнения независимых выборок, аналогичным t-критерию Стьюдента, является U-критерий Манна – Уитни:

(23)

Этот критерий не требует проверки на нормальность распределения, с его помощью можно сравнивать маленькие выборки объемом от 3 наблюдений. Также он подходит для сравнения выборок, данные в которых распределены ненормально.

Алгоритм расчета следующий:

1. Составить единый ранжированный ряд из обеих сопоставляемых выборок, расставив их элементы по степени нарастания признака и приписав меньшему значению меньший ранг. Общее количество рангов получится равным:

N = n₁ + n₂,

где n₁ – количество единиц в первой выборке;

n₂ – количество единиц во второй выборке.

2. Разделить единый ранжированный ряд на два, состоящие, соответственно, из единиц первой и второй выборок. Подсчитать отдельно сумму рангов, пришедшихся на долю элементов первой выборки, и отдельно – на долю элементов второй выборки. Определить большую из двух ранговых сумм (Tx), соответствующую выборке с nx единиц.

3. Определить значение U-критерия Манна – Уитни по формуле (23).

По таблице для избранного уровня статистической значимости определить критическое значение критерия для данных n₁ и n₂. Если полученное значение U меньше табличного или равно ему, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза). Если же полученное значение U больше табличного, принимается нулевая гипотеза. Достоверность различий тем выше, чем меньше значение U.

При справедливости нулевой гипотезы критерий имеет математическое ожидание и дисперсию 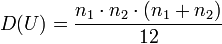и при достаточно большом объеме выборочных данных распределен практически нормально.

Коэффициент ассоциации φ используется для определения отношения между переменными, представленными в дихотомической шкале. Величина коэффициента φ лежит в интервале от –1 до 1, соответственно, он может принимать положительные и отрицательные значения, свидетельствуя о характере связи между дихотомическими переменными.

В общем виде формула вычисления коэффициента φ выглядит так:

(24)

где px – частота признака, имеющего 1 по x;

py – частота признака, имеющего 1 по y;

(1 – px) – частота признака, имеющего 0 по x;

(1 – py) – частота признака, имеющего 0 по y;

pxy – частота признака, имеющего 0 по x и 0 по y одновременно.

Применение данного коэффициента корреляции должно сопровождаться определением критических значений, для расчета которых применяется формула t-критерия Стьюдента:

(25)

где r_ЭМП – коэффициент корреляции, n – число коррелируемых признаков, а уровень значимости Т_Ф определяется по табл. II прил. 2, причем k = n – 2.

Коэффициент сопряженности Пирсона.Помимо коэффициента ассоциации, при проведении расчетов в случаях, когда обе переменные представляют собой дихотомическую шкалу, можно использовать коэффициент четырехклеточной сопряженности Пирсона:

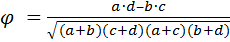(26)

Классификация объектов по дихотомической шкале приведет к построению четырехклеточной таблицы. К примеру, курсант может посетить более 50 % тренировок, а может и не посетить, может сдать зачет с первого раза, а может и не сдать. Данные для расчетов заносятся в таблицу.

Таблица 10

Показатель	Сдал зачет с первого раза	Не сдал зачет с первого раза
Курсант посещал тренировки	a	b
Курсант не посещал тренировки	c	d

В клетки a, b, c, d таблицы следует вписать количество объектов, обладающих соответствующими признаками. Приведенный коэффициент является модификацией коэффициента корреляции Пирсона, и расчет критических значений коэффициента сопряженности может быть произведен с помощью критических значений для коэффициента Пирсона, представленных в прил. 2.

Рангово-биссериальный коэффициент корреляции. Данный коэффициент применяется в случае, когда одна переменная измерена в дихотомической шкале, а другая – в ранговой. Особенностью данного коэффициента является то, что его знак, полученный на интервале от +1 до –1 не имеет никакого значения для интерпретации.

Расчет коэффициента рангово-биссериальной корреляции Rrb производится по формуле:

(27)

где

Х1 – средний ранг по элементам переменной Y, которым соответствует признак 1 в переменной X;

Х0 – средний ранг по элементам переменной Y, которым соответствует признак 0 в переменной Y;

N – общее количество элементов в переменной X.

Оценка уровня значимости коэффициента Rrb проводится по уже известной формуле (25).

Точечно-биссериальный коэффициент корреляции. Данный коэффициент корреляции применяется в тех случаях, когда одна переменная представлена в биссериальной шкале, а вторая – в шкале интервалов или отношений. Коэффициент может принимать значения от –1 до 1, но, как и в случае рангово-биссериальной корреляции, его знак не интерпретируется.

Для расчета коэффициента применяется формула: