Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
· Рассмотреть свойства арксинуса и арккосинуса;
· Рассмотреть свойства арктангенса и арккотангенса;
· Применять знания при решении задач.
Глоссарий по теме
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y). Он имеет область определения 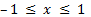 и множество значений
и множество значений 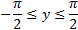 .
.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y). Он имеет область определения 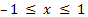 и множество значений
и множество значений 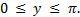
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y). Он имеет область определения 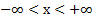 и множество значений
и множество значений 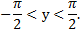 .
.
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y). Он имеет область определения 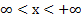 и множество значений
и множество значений 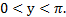
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Актуализация знаний
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен  ? Первое, что хочется ответить, что это угол 60° или
? Первое, что хочется ответить, что это угол 60° или  , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен
, но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен  , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
, бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Объяснение нового материала
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y).
| Свойства | Функции y=arcsin х |
| E(f) | 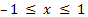
|
| D(f) | 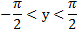
|
| Чётность | Нечётная, т.к. arcsin(-x)= - arcsin x |
| Промежутки монотонности | Возрастающая |
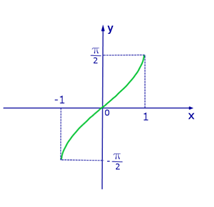
Рис.1 График функции y=arcsin х
Рассмотрим свойства функции y=arcos x и построим ее график.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y).
| Свойства | Функции y=arccos х |
| E(f) | 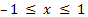
|
| D(f) | 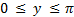
|
| Чётность | Ни чётная, ни нечётная |
| Промежутки монотонности | Убывающая |
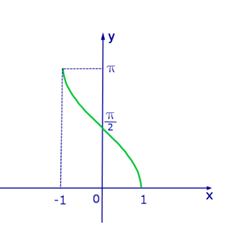
Рис.2 График функции y=arccos х
Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y).
Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y).
| Свойства | y=arctg х | y=arcctg х |
| E(f) | R | R |
| D(f) | 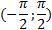
| 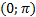
|
| Чётность | Нечётная | Нечётная |
| Промежутки монотонности | Возрастающая | Убывающая |
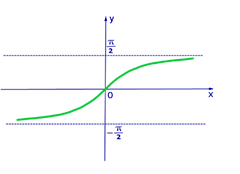
Рис.3 График функции y=arctgx
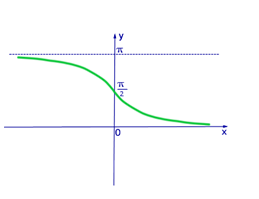
Рис.4 График функции y=arcсtgx
Вычисления значений аркфункций
Начнем с вычисления значений аркфункций.
Задача №1. Вычислить 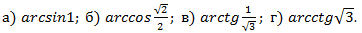
Как видим все аргументы аркфункций положительные и табличные, а это значит, что мы можем восстановить значение углов по первой части таблицы значений тригонометрических функций
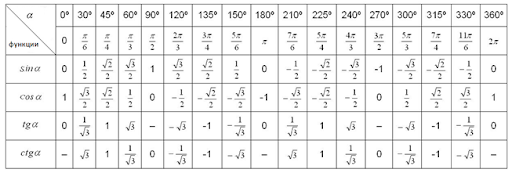
а) 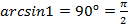
б) 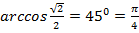
в) 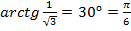
г) 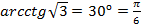
Ответ. 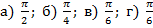 .
.
Задача №2. Вычислить 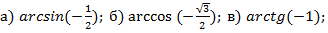
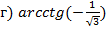 .
.
В данном примере мы уже видим отрицательные аргументы. В данном случае – это просто вынести минус из-под функции и просто свести задачу к предыдущей.
а) 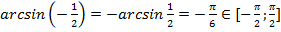
б) 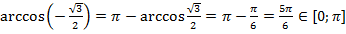
в) 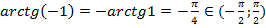
г) 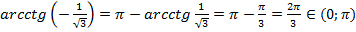
Ответ. 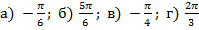 .
.
Задача №3. Вычислить 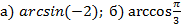 .
.
а) Первое, что необходимо заметить, это то, что аргумент арксинуса не входит в область определения
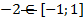 .
.
Следовательно, данная запись не имеет значения, и вычислить арксинус нельзя.
б)
вспомним, что 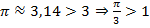 , т.е.
, т.е. 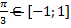 , а значит арккосинус не имеет смысла и вычислить его нельзя.
, а значит арккосинус не имеет смысла и вычислить его нельзя.
Ответ. Выражения не имеют смысла.
Задача №4. Вычислить 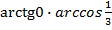 .
.
 2020-05-25
2020-05-25 72
72






