Выяснение общего характера и формы распределения предполагает количественную оценку степени его симметричности и однородности.
Симметричным является распределение, в котором частоты любых двух вариант, равноотстоящих по обе стороны от центра распределения, равны между собой. Для симметричных распределений имеет место равенство средней арифметической, моды и медианы. Чем больше разница между ними, тем больше асимметрия вариационного ряда. Ряд является умеренно асимметричным, когда разность между модой и средней примерно в три раза превышает разность между медианой и средней: 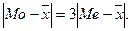
Для оценки степени асимметрии используется ряд других показателей:
1). Коэффициент асимметрии Пирсона (As):
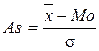 ,
,
где: 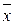 – средняя арифметическая;
– средняя арифметическая;
Мо – мода;
s – среднее квадратическое отклонение.
Величина этого показателя указывает на степень асимметрии распределения:
1). Если As = 0, (т. е. 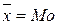 ), то распределение симметричное (нормальное).
), то распределение симметричное (нормальное).
2). Если As < 0 (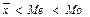 ), то имеет место левосторонняя асимметрия (левая ветвь кривой распределения относительно максимальной ординаты центра распределения вытянута больше, чем правая).
), то имеет место левосторонняя асимметрия (левая ветвь кривой распределения относительно максимальной ординаты центра распределения вытянута больше, чем правая).
3). Если As > 0 (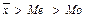 ), то имеет место правосторонняя асимметрия (правая ветвь кривой распределения относительно максимальной ординаты центра распределения вытянута больше, чем левая).
), то имеет место правосторонняя асимметрия (правая ветвь кривой распределения относительно максимальной ординаты центра распределения вытянута больше, чем левая).
Если | As | > 0,25, то асимметрия значительна; если | As | < 0,25 – незначительна.
 |
Рис. 4. Асимметрия распределения
2). Коэффициент асимметрии Линдберга:
As = П – 50,
где П – процент тех значений признака, которые превосходят по величине среднюю арифметическую.
3). Нормированный момент третьего порядка является показателем асимметрии распределения:
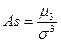 ,
,
где: μ3 – центральный момент распределения третьего порядка:
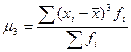 ;
;
s – среднее квадратическое отклонение.
Это наиболее точный показатель оценки асимметрии. В симметричном распределении величина μ3 равна нолю, поскольку варианты, равноудаленные от 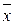 , имеют одинаковую частоту, а значит, и As равен нолю.
, имеют одинаковую частоту, а значит, и As равен нолю.
Если μ3 < 0, то в вариационном ряду преобладают (имеют большую частоту) варианты, которые меньше 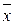 , т. е. ряд отрицательно ассиметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением μ3 > 0.
, т. е. ряд отрицательно ассиметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением μ3 > 0.
Степень существенности этого показателя асимметрии характеризуется средней квадратической ошибкой, которая зависит от объёма наблюдения n:
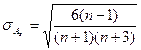 .
.
Если отношение 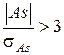 , то асимметрия существенна, если отношение
, то асимметрия существенна, если отношение 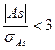 , то асимметрия несущественна, её наличие может быть объяснено влиянием различных случайных обстоятельств.
, то асимметрия несущественна, её наличие может быть объяснено влиянием различных случайных обстоятельств.
Однородные статистические совокупности характеризуются одновершинными распределениями. Многовершинность свидетельствует о неоднородности совокупности.
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс – высоковершинность или низковершинность фактической кривой распределения по сравнению с нормальным распределением.
Высоковершинность означает положительный эксцесс и характеризуется скоплением частот в середине. Низковершинность означает отрицательный эксцесс и характеризуется большой разбросанностью частот ряда.
1). Коэффициент эксцесса Линдберга (Ex):
Ex = П – 38,29,
где П – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения в ту или другую сторону от средней арифметической.
2). Нормированный момент четвёртого порядка как показатель эксцесса:
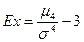 ,
,
где: μ4 – центральный момент распределения четвёртого порядка:
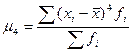 ;
;
s – среднее квадратическое отклонение.
Для нормального распределения нормированный момент четвёртого порядка равен 3, поэтому для оценки заострённости исследуемого распределения в сравнении с нормальным из него вычитается 3.
1). Если Ex = 0, то распределение симметрично.
2). Если Ex > 0 (ряд распределения с положительным эксцессом), то распределение островершинное.
3). Если Ex < 0 (ряд распределения с отрицательным эксцессом), то распределение плосковершинное (рис. 5).
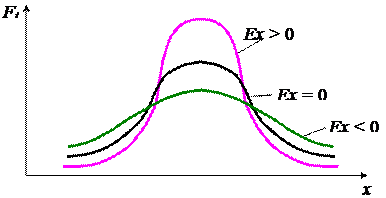 |
Рис. 5. Эксцесс распределения
Средняя квадратическая ошибка эксцесса зависит только от количества наблюдений n:
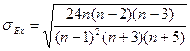 .
.
Степень приближённости вариационного ряда к нормальному распределению оценивается через числа Вестергарда, названные по имени датского статистика Харальда Людвига Вестергарда (1853-1936) (табл. 1).
Таблица 1. Числа Вестергарда
| Числа Вестергарда | Условия близости ряда к нормальному распределению | ||
| Интервалы | Объём совокупности, % | ||
| 0,3 | 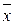 – 0,3s – 0,3s | 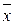 + 0,3s + 0,3s | 25 |
| 0,7 | 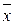 – 0,7s – 0,7s | 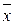 + 0,7s + 0,7s | 50 |
| 1,1 | 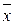 – 1,1s – 1,1s | 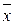 + 1,1s + 1,1s | 75 |
| 3,0 | 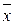 – 3,0s – 3,0s | 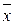 + 3,0s + 3,0s | 99 |
Пример 2.
Распределение фирм по объёму инвестиций в проекты представлено в таблице:
| Объём инвестиций, xi, млн руб. | Количество фирм, fi |
| 0 – 4 | 8 |
| 4 – 8 | 12 |
| 8 – 12 | 16 |
| 12 – 16 | 10 |
| 16 – 20 | 4 |
| Итого: | 50 |
Определить:
1) средний объём инвестиций;
2) моду;
3) дисперсию;
4) среднее квадратическое отклонение;
1). Средний объём инвестиций определяется по формуле средней арифметической взвешенной. В качестве значений xi берём середины соответствующих интервалов:
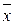 =
= 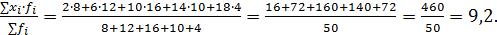
2). Модальным интервалом является третий (8 – 12), так как у него наибольшая частота в сравнении с другими интервалами – 16. Находим значение точечной моды:
Mo = 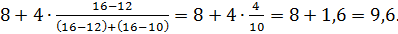
Для дальнейших расчётов составим вспомогательную таблицу:
| xi | fi | (xi – 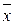 )2∙ fi )2∙ fi | (xi – 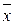 )3∙ fi )3∙ fi | (xi – 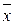 )4∙ fi )4∙ fi |
| 2 | 8 | (2–9,2)2∙8=414,72 | (2–9,2)3∙8=-2985,984 | (2–9,2)4∙8=21499,0848 |
| 6 | 12 | (6–9,2)2∙12=122,88 | (6–9,2)3∙12=-393,216 | (6–9,2)4∙12=1258,2912 |
| 10 | 16 | (10–9,2)2∙16=10,24 | (10–9,2)3∙16=8,192 | (10–9,2)4∙16=6,5536 |
| 14 | 10 | (14–9,2)2∙10=230,40 | (14–9,2)3∙10=1105,920 | (14–9,2)4∙10=5308,4160 |
| 18 | 4 | (18–9,2)2∙4=309,76 | (18–9,2)3∙4=2725,888 | (18–9,2)4∙4=23987,8144 |
| Итого: | 50 | 1088 | 460,8 | 52060,16 |
3). Дисперсия:
σ2 = 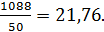
4). Среднее квадратическое отклонение:
σ = 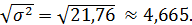
5). Коэффициент вариации:
v = 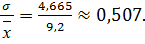
Вариация существенная.
а) по Пирсону:
As = 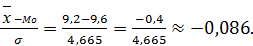
Незначительная левосторонняя асимметрия.
б) через нормированный момент третьего порядка:
μ3 = 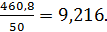
As = 
Незначительная правосторонняя асимметрия.
7). Коэффициент эксцесса определяется через нормированный момент четвёртого порядка:
μ4 = 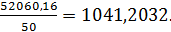
Ex = 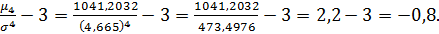
Распределение плосковершинное.
 2020-05-25
2020-05-25 1024
1024







