Тема 2. Показательные уравнения и неравенства

1. Простейшее показательное уравнение  имеет решение .

Пример 1. Решите уравнение .

Решение. Уравнение  является простейшим показательным уравнением, следовательно, имеет решение:      .

2.При решении показательных уравнений используется приём приведения левой и правой части уравнения к одному основанию, т.е. уравнение приводится к виду:

.

Пример 2. Решите уравнение .

Решение. Приводим правую и левую части уравнения к основанию 7:

Пример 3. Решите уравнение .

Решение. В левой части уравнения выносим за скобку , а в правой части :

.

Получаем уравнение . Основания показательных функций не совпадают. В левой части основание равно 6, а в правой 2. В этом случае необходимо разделить обе части уравнения на  или на . Делим обе части уравнения на :

.

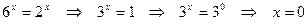Пример 4. Найдите сумму корней уравнения .

Решение. Находим область допустимых значений уравнения (ОДЗ), используя условие существования корня чётной степени: . Для значений  уравнение  равносильно совокупности двух уравнений:

Значение , тогда сумма корней уравнения .

Пример 5. Решите уравнение .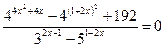

Решение. Находим область допустимых значений, используя условие существования дроби . Получаем:

.

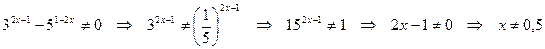Для значений  первоначальное уравнение равносильно уравнению:

.

Решаем уравнение:

.

Ответ: -1,5.

Пример 6. Решите уравнение .

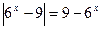Решение. Упростим уравнение . Так как левая часть неотрицательна, то . Отсюда следует  и уравнение принимает вид . Приравниваем каждый из множителей к нулю и решаем уравнения:

1) .

2)  - уравнение решений не имеет.

Ответ: .

3. Уравнение вида , где 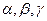 - числовые коэффициенты, с помощью замены , где t>0, сводится к квадратному уравнению .

Пример 7. Решите уравнение .

Решение. Приводим уравнение к виду , а затем делаем замену . Получаем квадратное уравнение . Находим корни данного уравнения  и . Корень  не удовлетворяет условию t>0. Для второго корня делаем обратную замену:                                .

4. Уравнение вида , где 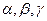 - числовые коэффициенты, называется однородным уравнением и сводится к квадратному уравнению с помощью почленного деления на  или на : .

Делаем замену  и получаем квадратное уравнение .

Пример 8. Решите уравнение .

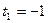Решение. Данное уравнение является однородным и приводится к виду . Делим обе части уравнения на  и получаем . В последнем уравнении делаем замену , в результате которой получаем квадратное уравнение , корнями которого являются числа -1 и . Корень  не удовлетворяет условию t>0. Для второго корня делаем обратную замену:                 .

5. При решении систем показательных уравнений используются приемы решения систем алгебраических уравнений, свойства степеней и приемы решения показательных уравнений.

Пример 9. Решите систему уравнений .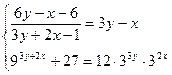

Решение. Область допустимых значений системы удовлетворяет неравенству: . Упростим второе уравнение системы . В результате замены переменных , получаем квадратное уравнение . Делаем обратную замену:

1) , но, согласно ОДЗ, .

2) .

Подставляем  в первое уравнение системы:

.

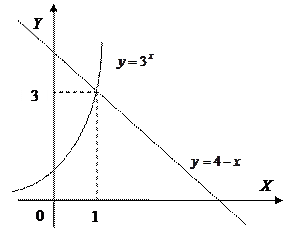6. Некоторые показательные уравнения решаются графическими методами. При этом находятся точки пересечения графиков функций, стоящих в левой и правой части уравнения.

Пример 10. Решите графически уравнение .

Решение. Функция  возрастает, а функция  убывает для всех , следовательно, графики этих функций имеют одну точку пересечения (1;3).

Решение показательных неравенств основано на свойстве монотонности функции . Возможны два случая: 1.

2.

Пример 11. Найдите наибольшее целое значение x, удовлетворяющее неравенству .

Решение. Приводим левую и правую части неравенства к основанию 3:

.

Знак неравенства не меняется, так как основание 3>1. Решаем полученное неравенство:

.

Решением неравенства является промежуток , наибольшее целое значение x из этого промежутка равно -2.

Пример 12. Найдите область определения функции .

Решение. Область определения функции удовлетворяет условию существования корня чётной степени . Решаем полученное неравенство:

.

Так как основание , то при переходе к показателям степеней знак неравенства меняется на противоположный. Областью определения функции  является множество .

Пример 13. Найдите наименьшее целое значение x, удовлетворяющее неравенству .

Решение. Переносим все функции с основанием 2 в левую часть неравенства, а с основанием 5 – в правую часть неравенства и выносим общие множители за скобки:

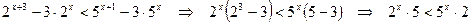
Разделим обе части полученного неравенства на :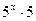

.

Знак неравенства меняется, так как основание . Получаем, что . Наименьшим целым решением неравенства является x= 2.

Пример 14. Решите неравенство .

Решение. Приводим неравенство к следующему виду:

.

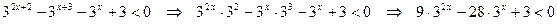Делаем замену  и получаем квадратное неравенство . Корни соответствующего квадратного уравнения 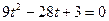 равны  и . Находим решение квадратного неравенства. Решением квадратного неравенства является интервал . В результате обратной замены получаем неравенство .

Задачи.

1. Укажите промежуток, которому принадлежит корень уравнения .

1)

2)

3)

4)

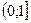
2. Укажите промежуток, которому принадлежит корень уравнения .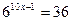

1)

2)

3)

4)

3. Сумма корней уравнения  равна

1)

2)

3)

4)

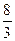
4. Сумма корней уравнения  равна

1)

2)

3)

4)

5. Произведение корней уравнения  равно

1) -1                             2) 2                               3) -3                            4)

6. Сумма корней уравнения  равна

1) 4

2) -4

3) 3

4) -3

7. Произведение корней уравнения равно

1) 2

5) 8

9) -4

2) -2

6) 1

10) 5

3) -6

7) 6

11) -5

4) 4

8) -1

12) -8

8. Корень уравнения равен

1) 1/3

5) 1

9) -5/3

2) -1/3

6) -1

10) 5/3

3) -2/3

7) -4/3

11) 2

4) 2/3

8) 4/3

12) -2

9. Корень уравнения равен

1) 1

5) 3

9) 6

2) -1

6) -3

10) -6

3) 2

7) 1,5

11) 2,5

4) -2

8) -1,5

12)-2,5

10. Если  – корень уравнения , то значение выражения  равно

1) 2

5) 4

9) -4

2) -2

6) 5

10) -5

3) 1

7) 3

11) -3

4 -1

8) 6

12) -6

11. Найдите среднее арифметическое всех корней уравнения .

1)

2)

3)

4)

12. Найдите среднее арифметическое всех корней уравнения .

1)

2)

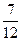
3)

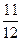
4)

13. Найдите сумму корней уравнения .

14. Найдите наибольший корень уравнения .

15. Произведение корней уравнения  равно

1) 2

5) 3

2) 4,5

6) -2

3) -3

7) -4,5

4) -2,5

8) 2,5

16. Укажите промежуток, которому принадлежит корень уравнения

1) (1;3)

5) (-4;-3)

2) (2;4)

6) (0;1)

3) (3;4)

7) (-2;0)

4) (4;5)

8) (-3;-1)

17. Укажите промежуток, которому принадлежит корень уравнения

1) [-2;0];                       2) (0;1);                       3) (2;3);                     4) [1;2].

18. Решите уравнения:

1)                                               2)

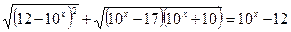3)           4)

19. Решите системы уравнений:

1)

2)

20. Решите неравенство

21. Количество целых решений неравенства равно

1) 0

5) 4

2) 1

6) 5

3) 2

7) 6

4) 3

8) 7

22. Найдите область определения функции

1)                        2)                       3)                     4)

23. Найдите область определения функции

24. Найдите область определения функции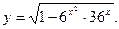

1) [-2;0]                       2) [0;2]                       3)        4) [-2;2]

25. Найдите область определения функции .

1)

2)

3)

4)

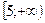
26. Наибольшее целое решение неравенства  равно

1) 3

5) -3

2) -1

6) 0

3) 2

7) -2

4) 4

8) 1

27. Найдите количество целых решений неравенства .

28. Найдите сумму целых решений неравенства .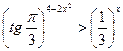

29. Найдите число целых решений неравенства

30. Найдите сумму целых решений неравенства .

31. Найдите сумму всех целых решений неравенства .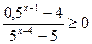

32. Найдите сумму всех целых решений неравенства .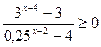

33. Найдите все значения x, при каждом из которых произведение значений выражений  и  положительно.

34. Найдите все значения x, при каждом из которых произведение значений выражени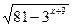й  и 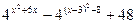 положительно.

35. Найдите все значения x, при которых точки графика функции  лежат ниже соответствующих точек графика функции .

36. Решите уравнения и неравенства:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)