Жесткие системы дифференциальных уравнений

Лекция 8. Решение систем ОДУ и двухточечных краевых задач для ОДУ

В MathCAD

1. Решение систем обыкновенных дифференциальных уравнений.

Для численного интегрирования систем ОДУ в MathCAD также имеется выбор – либо использовать вычислительный блок Given/Odesolve, либо встроенные функции rkfixed, Rkadapt и Bulstoer.

При решении систем ОДУ MathCAD требует, чтобы система ОДУ была представлена в нормальной форме (когда левые части – первые производные от соответствующих функций, а в правых частях производные отсутствуют):

где Y и Y’ – соответствующие неизвестные векторные функции переменной t, а F – вектор правых частей системы уравнений первого порядка. Именно векторное представление используется для ввода системы ОДУ в среде MathCAD.

Если в систему ОДУ входят и уравнения высших порядков, то оно тоже сводится к системе уравнений первого порядка, как было показано выше. При этом количество нулевых условий для вычислительного блока Given/Odesolve, а также размер вектора начальных условий y и размер вектора правых частей F(x,y) для встроенных функций rkfixed, Rkadapt и Bulstoer должны быть равны сумме порядков всех уравнений.

Вначале покажем решение систем ОДУ первого порядка с использованием вычислительного блока Given/Odesolve

Функция Odesolve для системы ОДУ имеет несколько иной, по сравнению с одним уравнением, синтаксис. Теперь она возвращает вектор функций, составляющих решение системы. Поэтому в качестве первого аргумента функции нужно ввести вектор, состоящий из имен функций, использованных при вводе системы. Второй и третий аргументы то же самое, что и в задаче с одним ОДУ.

Решение системы ОДУ показано на графике слева. Как известно, решения ОДУ часто удобнее изображать не в таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций (как показано на рисунке справа). При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такой график – фазовый портрет системы – является кривой на фазовой плоскости. В общем случае, если система состоит из N ОДУ, то фазовое пространство является N – мерным. При N > 3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.

Рассмотрим решение этой же системы ОДУ первого порядка с использованием встроенной функции rkfixed.

Полученное решение полностью соответствует вышеприведенному решению с использованием вычислительного блока Given/Odesolve. Следует отметить, что начальные условия здесь задаются в виде вектора y, а функциям x(t) и y(t) соответствуют элементы этого вектора y₁ и y₂. Вектор начальных условий y и вектор правых частей F имеют размер равный двум, т.к. система состоит из двух уравнений первого порядка. Для системы ОДУ, состоящей из двух уравнений второго порядка, размер этих векторов будет равен четырем

2. Решение жестких ОДУ и систем ОДУ.

Сложно дать математически точное определение жесткости, поскольку задачи, входящие в этот класс, весьма разнообразны. Чаще всего жесткими дифференциальными уравнениями называются уравнения, в решении которых есть плавно меняющаяся компонента, а также быстро затухающие возмущения.

Жесткие системы дифференциальных уравнений

В некоторых системах дифференциальных уравнений описанные ранее методы численного решения дают плохие результаты. А именно, для достижения заданной точности приходится выбирать очень мелкий шаг, т.е. выполнять слишком большой объем вычислений. К таким системам относятся жесткие системы дифференциальных уравнений.

Определение. Система дифференциальных уравнений (7) называется жесткой вдоль решения y = j(x), если выполняются следующие два условия:

1. собственные числа l_k матрицы  имеют отрицательные действительные части при любом x;

2. число жесткости велико.

Собственными числами матрицы являются корни уравнения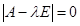  

Напомним, что матрица  – это матрица Якоби, т.е. матрица из частных производных, элементы которой имеют вид . Перед вычислением собственных чисел в эти элементы вместо y нужно подставить y = j(x), т.е. то решение, вдоль которого исследуется система на жесткость. Полученная матрица будет зависеть только от x, и ее собственные числа тоже будут зависеть от x. Условие 2 в определении жесткой системы оставляет некоторый произвол в понимании слова «велико». Насколько велико должно быть число жесткости g, определяется в зависимости от конкретной задачи. Обычно система считается жесткой, если число жесткости порядка нескольких сотен. Если система (7) – линейная, то матрица A(x,y) зависит только от x, а если система линейная с постоянными коэффициентами, то эта матрица является постоянной, т.е. числовой (наиболее простой случай). Для линейных систем условие жесткости не зависит от рассматриваемого решения.

Вот цитата из посвященной жестким уравнениям монографии К. Деккера и Я. Вервера: «Сущность явления жесткости состоит в том, что решение, которое нужно вычислить, меняется медленно, однако существуют быстро затухающие возмущения. Наличие таких возмущений затрудняет получение медленно меняющегося решения численным способом».

Для решения жестких систем дифференциальных уравнений разработаны специальные методы. Они используют неявные схемы типа интерполяционных методов, указанных выше, и используют матрицу Якоби правых частей системы уравнений.

Возможны случаи, когда система дифференциальных уравнений является жесткой только на какой-то части решения, а на остальной части жесткой не является. В этом случае можно первую часть решения найти с помощью методов для жестких систем, а другую часть – с помощью методов, описанных выше.

 

Для жестких систем (stiff) не работает обычный метод Рунге-Кутта или Булирша-Штера. Наличие быстро затухающего возмущения приводит к тому, что эти численные методы дают расходящееся решение. Для жестких задач разрабатываются специальные методы. В MathCAD предусмотрены три различные функции для решения жестких задач:

- Radau – метод Radaus для жестких систем. Полностью аналогичен использованию функции odesolve с выбранным в контекстном меню методом Stiff.

- Stiffb – метод Булирша-Штера, адаптированный для жестких систем.

- Stiffr – метод Розенброка.

3. Краевые задачи для ОДУ

Постановка краевых задач для ОДУ отличается от задач Коши, рассмотренных выше, тем, что граничные условия для них ставятся не в одной начальной точке, а на обеих границах расчетного интервала. Если имеется система N ОДУ первого порядка, то часть из N условий может быть поставлена на одной границе интервала, а оставшиеся условия – на противоположной границе. В связи с тем, что условия поставлены не на одной, а на обеих границах интервала, краевые задачи нельзя решить изложенными выше методами, предназначенными для задач Коши. Для решения краевой задачи в MathCAD нет отдельной функции. Однако есть функции, позволяющие превратить краевую задачу в задачу Коши. Эти функции «угадывают» недостающие начальные условия, исходя из того, что решение должно удовлетворять заданным условиям в конечной точке интервала интегрирования. Простейшей из функций, предназначенных для приведения краевой задачи к задаче Коши, является функция sbval.

Для того, чтобы решить двухточечную краевую задачу с помощью этой функции, следует выполнить следующие действия:

1. Задайте вектор v с количеством элементов равным количеству недостающих начальных условий. Значения элементов этого вектора – это начальные приближения, исходя из которых будет происходить поиск недостающих начальных условий. На данном этапе не конкретизируется, какой из элементов вектора будет соответствовать начальному значению той или иной неизвестной функции в задаче.

2. Задайте функцию F (x,y). Эта функция уже описывалась выше. Она представляет собой вектор, каждый элемент которого – это правая часть одного из уравнений системы.

3. Задайте еще одну векторную функцию load (x,v). Это функция от скалярного аргумента x и вектора v, который имеет столько же компонент, сколько недостающих начальных условий в системе. Сам вектор load должен содержать такое же количество элементов, как и вектор F, т.е. столько, сколько должно быть начальных условий в задаче. Если начальное значение какой-либо из функций известно, то соответствующий элемент вектора load должен содержать это значение. Для функций, начальное значение которых неизвестно, соответствующий элемент вектора load должен содержать один из элементов вектора v.

4. Следует задать еще одну некоторую функцию score (x,y). Аргументы этой функции – скаляр x и вектор y, который имеет столько элементов, сколько уравнений в системе. Количество компонент вектора score должно равняться количеству граничных условий, заданных в конечной точке отрезка интегрирования. На самом деле каждая компонента этого вектора задает одно из граничных условий в конечной точке. Например, если в задаче есть граничной условие y_i(b)=c, то один из элементов вектора score должен быть функцией, которая обращается в нуль при значениях x=b и y(b)=c. Конкретный вид этой функции не играет особой роли, поэтому проще всего задавать ее в таком виде: score_k(x,y):=y_i-c. Таким же образом должны быть заданы все элементы вектора score для всех конечных условий задачи.

5. Теперь все введенные величины нужно использовать как аргументы в функции sbval. Использование этой функции выглядит следующим образом: Y:=sbval(v,a,b,F,load,score). Аргументы a и b – это начало и конец отрезка интегрирования.

6. Результатом функции sbval будет вектор, содержащий недостающие начальные значения. Их последовательность задается той последовательностью, в которой были использованы компоненты вектора v в функции load.

7. Постройте вектор начальных значений, используя известные начальные значения, а также элементы вектора Y, там, где значения были неизвестны.

8. Теперь можно решить полученную задачу как задачу Коши, с помощью, например, функции Rkadapt.

Ниже приведено решение дифференциального уравнения на отрезке [0,3] с начальным условием y(0)=1 и граничным условием y(3)=4. Недостающее начальное условие – y’(0).