Практическое занятие № 3
Геометрическое определение вероятности применяется в случае, когда число исходов опыта бесконечно.
Пусть каждому исходу опыта поставлена в соответствие точка плоскости 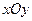 . Тогда множеству всех исходов опыта соответствует область
. Тогда множеству всех исходов опыта соответствует область 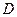 плоскости
плоскости 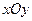 , а множеству исходов, благоприятствующих появлению события
, а множеству исходов, благоприятствующих появлению события 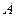 , соответствует область
, соответствует область 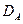 плоскости
плоскости  . Будем считать, что все исходы опыта равновозможны, несовместны и образуют полную группу.
. Будем считать, что все исходы опыта равновозможны, несовместны и образуют полную группу.
Тогда вероятность события  вычисляется по формуле:
вычисляется по формуле: 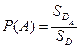 , где
, где 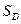 - площадь области
- площадь области 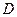 ;
;
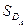 - площадь области
- площадь области 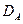 .
.
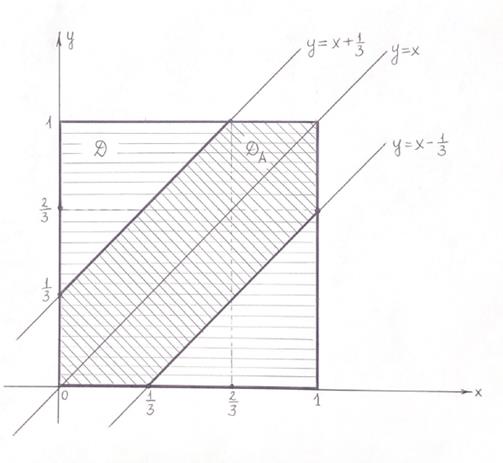
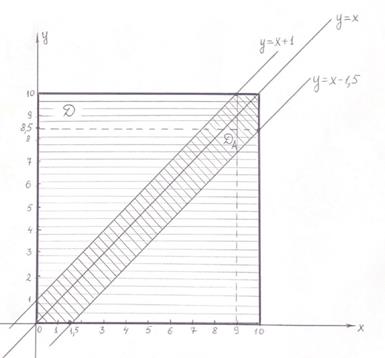
Задача 1. Наугад взяты два положительных числа, каждое из которых не больше единицы.
Какова вероятность того, что их сумма не превосходит единицы, а их произведение не больше 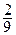 ?
?
Обозначим: первое число 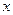 ,
,
второе число 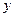 .
.
Событие 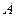 - сумма
- сумма 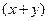 не превосходит единицы, а произведение
не превосходит единицы, а произведение 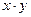 не больше
не больше 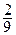 .
.
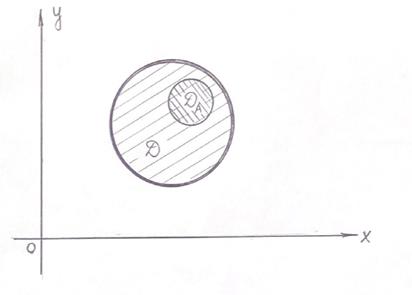
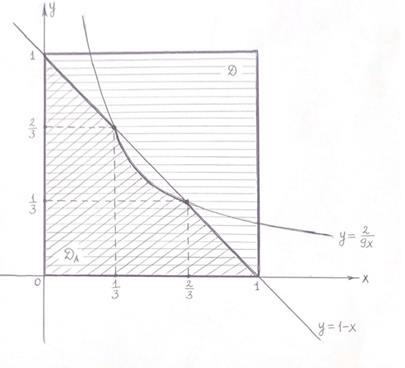
Общее число исходов опыта описывается системой неравенств: 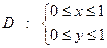 (1)
(1)
Область 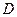 , описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми
, описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми 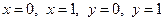 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 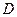 равна:
равна: 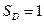 .
.
Число исходов, благоприятствующих событию  , описывается системой неравенств:
, описывается системой неравенств:
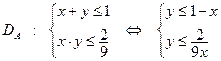
Площадь области  (см. рисунок) равна:
(см. рисунок) равна:
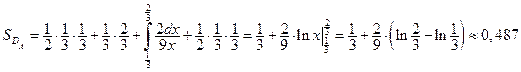 .
.
Тогда вероятность события 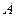 равна:
равна: 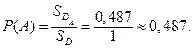
Задача 2. Наугад взяты два положительных числа 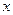 и
и 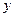 , каждое из которых не превышает двух.
, каждое из которых не превышает двух.
Найти вероятность того, что произведение 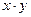 будет не больше единицы, а частное
будет не больше единицы, а частное 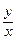 не больше двух.
не больше двух.
Событие 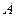 - произведение
- произведение 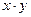 будет не больше единицы, а частное
будет не больше единицы, а частное 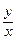 не больше двух.
не больше двух.
Общее число исходов опыта описывается системой неравенств: 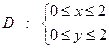 (1)
(1)
Область 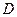 , описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми
, описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми 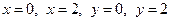 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 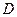 равна:
равна: 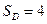 .
.
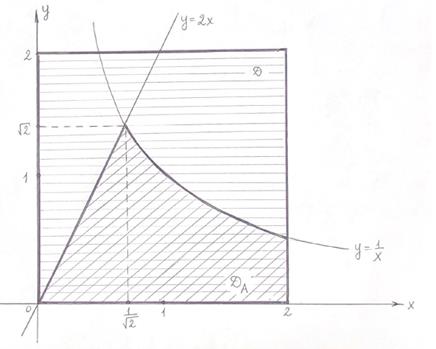
Число исходов, благоприятствующих событию 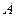 , описывается системой неравенств:
, описывается системой неравенств:
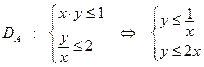 (2)
(2)
Область 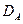 , описываемая системой неравенств (2), представляет собой криволинейную трапецию, ограниченный линиями
, описываемая системой неравенств (2), представляет собой криволинейную трапецию, ограниченный линиями 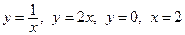 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 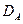 равна:
равна: 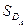 равна:
равна:
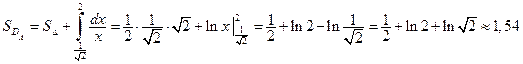 .
.
Тогда вероятность события 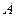 равна:
равна: 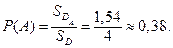
Задача 3. На отрезке  длины
длины  числовой оси
числовой оси 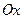 наудачу поставлены две точки
наудачу поставлены две точки 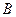 и
и 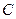 .
.
Найти вероятность того, из трех получившихся отрезков можно построить треугольник.
Событие 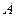 - из трех отрезков можно построить треугольник.
- из трех отрезков можно построить треугольник.
Обозначим: длину первого отрезка 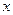 ,
,
длину второго отрезка 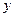 ,
,
длину третьего отрезка 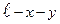 .
.
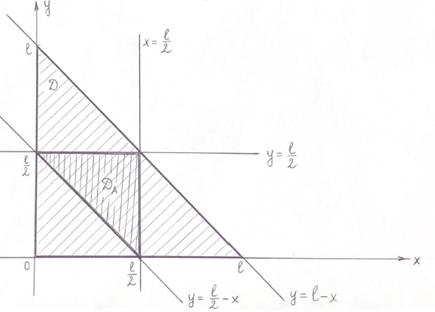
Общее число исходов опыта описывается системой неравенств: 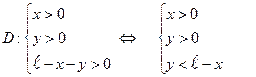 (1)
(1)
Область 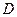 , описываемая системой неравенств (1), представляет собой треугольник, ограниченный прямыми
, описываемая системой неравенств (1), представляет собой треугольник, ограниченный прямыми 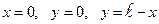 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 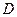 равна:
равна: 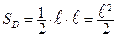 .
.
Теорема. Сумма длин двух любых сторон треугольника больше длины третьей стороны.
Тогда число исходов, благоприятствующих событию 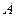 , описывается системой неравенств:
, описывается системой неравенств:
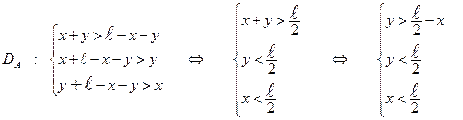 (2)
(2)
Область 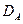 , описываемая системой неравенств (2), представляет собой треугольник, ограниченный прямыми
, описываемая системой неравенств (2), представляет собой треугольник, ограниченный прямыми 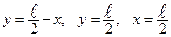 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 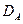 равна:
равна: 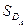 равна:
равна: 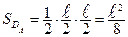 .
.
Тогда вероятность события 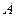 равна:
равна: 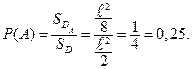
Задача 4. Два студента договорились встретиться между 12 и 13 часами. Пришедший первым ждет второго 20 минут  , после чего уходит.
, после чего уходит.
Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода в указанном промежутке.
Событие  - студенты встретятся.
- студенты встретятся.
Пусть 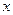 и
и 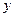 - моменты прихода студентов на встречу.
- моменты прихода студентов на встречу.
Общее число исходов опыта описывается системой неравенств: 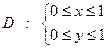 (1)
(1)
Область 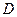 , описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми
, описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми 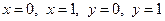 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 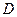 равна:
равна: 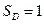 .
.
Число исходов, благоприятствующих событию 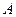 (студенты встретятся), описывается неравенствами:
(студенты встретятся), описывается неравенствами:
1) если студент 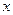 приходит первым и ждет студента
приходит первым и ждет студента 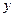 20 минут
20 минут 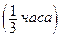 , то
, то 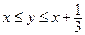 ;
;
2) если студент 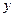 приходит первым и ждет студента
приходит первым и ждет студента 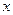 20 минут
20 минут 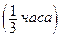 , то
, то 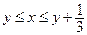 .
.
Площадь области 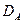 (см. рисунок) равна:
(см. рисунок) равна: 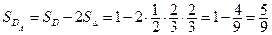 .
.
Тогда вероятность события 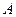 равна:
равна: 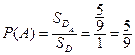 .
.
Задача 5. Автобусы маршрутов  и
и  прибывают на остановку в случайные моменты времени на каждом десятиминутном интервале. Стоянка автобуса
прибывают на остановку в случайные моменты времени на каждом десятиминутном интервале. Стоянка автобуса  - одна минута, автобуса
- одна минута, автобуса 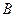 - полторы минуты.
- полторы минуты.
Найти вероятность встречи автобусов на этой остановке, если моменты прихода каждого из них независимы и равновозможны в течение указанного времени.
Событие 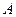 - автобусы встретятся на остановке.
- автобусы встретятся на остановке.
Пусть 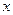 и
и 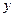 - моменты прихода автобусов
- моменты прихода автобусов 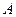 и
и 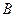 на остановку.
на остановку.
Общее число исходов опыта описывается системой неравенств: 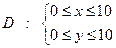 (1)
(1)
Область 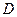 , описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми
, описываемая системой неравенств (1), представляет собой квадрат, ограниченный прямыми 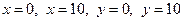 (см. рисунок).
(см. рисунок).
Следовательно, площадь области 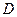 равна:
равна: 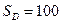 .
.
Число исходов, благоприятствующих событию 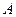 , описывается неравенствами:
, описывается неравенствами:
1) если автобус  приходит первым и стоит одну минуту, то
приходит первым и стоит одну минуту, то 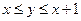 ;
;
2) если автобус  приходит первым и стоит полторы минуты, то
приходит первым и стоит полторы минуты, то 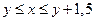 .
.
Площадь области 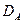 (см. рисунок) равна:
(см. рисунок) равна:
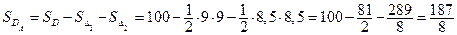 .
.
Тогда вероятность события 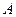 равна:
равна: 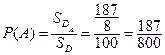 .
.
Статистическое определение вероятности
Классическое и геометрическое определения вероятности основаны на предположении, что все исходы опыта равновозможны. На практике доказать или опровергнуть это предположение затруднительно.
Тогда применяют статистическое определение вероятности, где в качестве вероятности события принимают его относительную частоту или частость.
Пусть опыт проводится 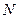 раз при одинаковых условиях, и пусть в этом опыте событие
раз при одинаковых условиях, и пусть в этом опыте событие 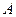 наступило
наступило 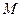 раз. Тогда отношение числа опытов
раз. Тогда отношение числа опытов 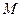 , в которых наступило событие
, в которых наступило событие 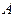 , к общему числу опытов
, к общему числу опытов 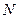 называется частостью события
называется частостью события 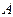 или относительной частотой события
или относительной частотой события 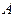 :
:
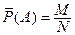
В другой серии опытов частость события 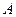 может иметь другое значение. Но при увеличении числа опытов
может иметь другое значение. Но при увеличении числа опытов 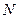 частость события
частость события 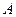 стабилизируется и обладает статистической устойчивостью. В силу этого частость события
стабилизируется и обладает статистической устойчивостью. В силу этого частость события 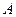 приближенно принимают равной вероятности события
приближенно принимают равной вероятности события 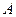 в единичном опыте:
в единичном опыте:
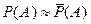
Задача 1. По цели произвели 20 выстрелов, при этом было зарегистрировано 18 попаданий в цель.
Найти вероятность попадания в цель при одном выстреле.
Событие 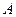 - попадание в цель при одном выстреле.
- попадание в цель при одном выстреле.
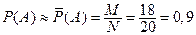
Задача 2. При испытании партии приборов относительная частота годных оказалась равной 0,9.
Найти число годных приборов, если всего было проверено 200 штук.
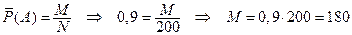 - число годных приборов в партии из 200 штук.
- число годных приборов в партии из 200 штук.
 2020-05-25
2020-05-25 432
432






