Практическая работа по теме «Построение таблиц истинности»
Цель работы: научиться строить таблицы истинности сложных высказываний.
Ход работы:
Вспомним таблицы истинности основных логических операций:
Инверсия (отрицание): образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно что».
| Х | 
|
| 1 | 0 |
| 0 | 1 |
Дизъюнкция (сложение): образуется соединением двух высказываний в одно с помощью союза «или»
| X | Y | X V Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Импликация (следование): логическая функция от двух переменных, которая принимает нулевое значение, когда из истины следует ложь.
| X | Y | X Þ Y |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Конъюнкция (умножение): образуется соединением двух высказываний в одно с помощью союза «и»
| X | Y | X & Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Эквивалентность (равнозначность): Логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных.
| X | Y | XÛY |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Опорный конспект
| Инверсия истинна | тогда | Высказывание ложно |
| Дизъюнкция ложна Конъюнкция истинна | и | Оба ложны высказывания истинны |
| Конъюнкция истинна Дизъюнкция ложна | только | Хотя бы одно истинно высказывание ложно |
| Импликация ложна | тогда, | Из истинного высказывания следует ложное высказывание |
| Эквивалентность истинна | когда | Обавысказывания ложныили обавысказывания истинны |
Порядок выполнения операций
1. Логическое отрицание - инверсия (НЕ)
2. Логическое умножение - конъюнкция (И)
3. Логическое сложение - дизъюнкция (ИЛИ)
4. Логическое следование - импликация
5. Равнозначность - эквивалентность
Алгоритм построения таблицы истинности
1. Вычислить количество строк (2n+1, где n-кол-во простых высказываний) и столбцов таблицы (сумма переменных и операций).
2. Начертить таблицу и заполнить заголовок.
3. Заполнить столбцы значений переменных.
4. Заполнить остальные столбцы в соответствии с таблицами истинности соответствующих операций.
Примеры:
1.Построить таблицу истинности логической функции F=(A Ú B)Ù (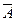 Ú
Ú  )
)
В этой функции две переменные (A и B), значит в таблице истинности будет 22+1=5 строк и 2+5(операций)=7 столбцов. Построим таблицу:
| A | B | 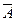
| 
| A Ú B | 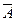 Ú Ú 
|
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
Продолжим заполнение таблицы в соответствии с таблицами истинности логических операций:
| A | B | 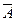
| 
| A Ú B | 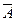 Ú Ú 
|
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
Готовую работу прислать на Фото выполненной работы отправить не позднее 28 апреля на почту yulyashka310887@mail.ru или в личные сообщения https://vk.com/id590938749
 2020-05-25
2020-05-25 323
323






