2020-05-25
106
- Если функцией является перемещение тела, то производная от этой функции – скорость
- Если функцией является скорость, то производная от этой функции – ускорение
Пример: Материальная точка движется по закону 
. Найти мгновенную скорость в момент 
Скорость v – производная от перемещения s: 
. При t=5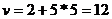 
Связь графиков функции и производной
| Производная | Функция | Касательная к графику функции | ||||
| Положительна | Возрастает | Наклонена вправо (острый угол с осью Х) | ||||
| Отрицательна | Убывает | Наклонена влево (тупой угол с осью Х) | ||||
| Равна нулю (с вариантами) | Стационарная точка | Горизонтальна (параллельна оси Х) | ||||
| =0, меняет знак с минуса на плюс | Минимум (экстремум) | |||||
| =0, меняет знак с плюса на минус | Максимум (экстремум) | |||||
| =0, но знак не меняет | Точка перегиба | |||||
| На рисунке изображен график |
| |||||
| 1) Выделяем нужный отрезок (если он задан) 2) В точках, где производная равна 0, проводим вертикальные линии 3) Схематически (стрелками) рисуем функцию: там, где производная положительна, возрастающую, а где отрицательна – убывающую 4) СМОТРИМ ТОЛЬКО НА ЭТИ СТРЕЛКИ и отвечаем на вопрос На отмеченном отрезке [-6; 9] максимум у функции один – в точке 7. Ответ: 1
|
| |||||
— производной функции 
Если дан график функции, а спрашивают про производную
На рисунке изображен график функции  , определенной на интервале (-6; 8). Найти количество целых точек, где производная положительна
| 
|
| 1) Выделяем нужный отрезок (если он задан) 2) В точках, где функция имеет максимумы или минимумы, проводим вертикальные линии 3) Схематически рисуем производную: там, где функция возрастает – положительная волна, а где убывает – отрицательная 4) СМОТРИМ ТОЛЬКО НА ЭТИ ВОЛНЫ и отвечаем на вопрос Производная положительна в точках -2, -1, 5, 6. То есть всего 4 точки. Ответ: 4 | 
|
Домашнее задание. №30.25,№30.8 (по желанию)
