2020-05-25
467
Задание:
1. Написать конспект.
2. Выполнить задание.
На данном занятии мы рассмотрим важное следствие теорем сложения и умножения вероятностей и научимся решать типовые задачи по теме.
Рассмотрим зависимое событие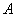 
, которое может произойти лишь в результате осуществления одной из несовместных гипотез 
, которые образуют полную группу. Пусть известны их вероятности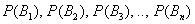 
и соответствующие условные вероятности 
. Тогда вероятность наступления события 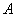равна:
Эта формула получила название формулы полной вероятности. В учебниках она формулируется теоремой, доказательство которой элементарно: согласно алгебре событий, 
(произошло событие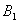 
и после него наступило событие 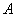или произошло событие 
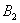и после него наступило событие 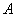или произошло событие 
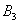и после него наступило событие 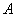или …. или произошло событие 
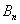и после него наступило событие 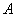). Поскольку гипотезы несовместны, а событие 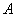– зависимо, то по теореме сложения вероятностей несовместных событий (первый шаг) и теореме умножения вероятностей зависимых событий (второй шаг):
|
|
|
Задача 1
Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный?
Решение: рассмотрим событие 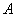– из наугад выбранной урны будет извлечён чёрный шар. Данное событие может произойти или не произойти в результате осуществления одной из следующих гипотез:
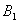– будет выбрана 1-я урна;
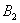– будет выбрана 2-я урна;
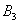– будет выбрана 3-я урна.
Так как урна выбирается наугад, то выбор любой из трёх урн равновозможен, следовательно: 
Обратите внимание, что перечисленные гипотезы образуют полную группу событий, то есть, по условию чёрный шар может появиться только из этих урн. Проведём простую промежуточную проверку: 
Идем дальше:
В первой урне 4 белых + 7 черных = 11 шаров, по классическому определению: 
– вероятность извлечения чёрного шара при условии, что будет выбрана 1-я урна.
Во второй урне только белые шары, поэтому в случае её выбора появление чёрного шара становится невозможным: 
.
И, наконец, в третьей урне одни чёрные шары, а значит, соответствующая условная вероятность извлечения чёрного шара составит 
(событие достоверно).
По формуле полной вероятности: 
– вероятность того, что из наугад выбранной урны будет извлечен чёрный шар.
Ответ: 
Задача 2 См. решение
В тире имеются 5 различных по точности боя винтовок. Вероятности попадания в мишень для данного стрелка соответственно равны 0,5; 0,55; 0,7; 0,75 и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки?
|
|
|
Решение: рассмотрим гипотезы 
, состоящие в том, что стрелок выберет 1-ю, 2-ю, 3-ю, 4-ю и 5-ю винтовку соответственно. Выбор любой винтовки равновозможен, следовательно:
______________
Рассмотрим событие 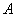– стрелок попадёт в мишень из наугад взятой винтовки.
По условию:
.
По формуле полной вероятности:
_____________________________________________________________
Ответ: ______
В большинстве тематических задач гипотезы, конечно же, не равновероятны:
Задача 3
В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки.
Решение: в этой задаче количество винтовок точно такое же, как и в предыдущей, но вот гипотезы всего две:
– стрелок выберет винтовку с оптическим прицелом;
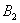– стрелок выберет винтовку без оптического прицела.
По классическому определению вероятности:
.
Контроль: 
Рассмотрим событие: 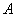– стрелок поразит мишень из наугад взятой винтовки.
По условию: 
.
По формуле полной вероятности:
Ответ: 0,85
На практике вполне допустим укороченный способ оформления задачи, который вам тоже хорошо знаком:
Решение: по классическому определению: 
– вероятности выбора винтовки с оптическим и без оптического прицела соответственно.
По условию, 
– вероятности попадания в мишень из соответствующих типов винтовок.
По формуле полной вероятности:
– вероятность того, что стрелок поразит мишень из наугад выбранной винтовки.
Ответ: 0,85
Задача 4 См. решение
Двигатель работает в трёх режимах: нормальном, форсированном и на холостом ходу. В режиме холостого хода вероятность его выхода из строя равна 0,05, при нормальном режиме работы – 0,1, а при форсированном – 0,7. 70% времени двигатель работает в нормальном режиме, а 20% – в форсированном. Какова вероятность выхода из строя двигателя во время работы?
Напомню – чтобы получить значения вероятностей проценты нужно разделить на 100
Решение: из условия находим 
– вероятности того, что двигатель работает на холостом ходу, в нормальном и форсированном режимах соответственно. По условию 
– вероятности выхода из строя двигателя для холостого, нормального и форсированного режима соответственно. По формуле полной вероятности: 
____________________ – вероятность того, что двигатель выйдет из строя
Ответ: ________
