Проверка адекватности модели

Лекция 11

Тема: Задача баскетболиста ( продолжение )

Аналитическое решение задачи баскетболиста

Для получения решения рассмотренной выше задачи баскетболиста в постановке (2.5) - (2.8) можно использовать как аналитические, так и численные методы. Проинтегрировав соотношения (2.5) по времени, получим

                   (2.9)

Постоянные интегрирования найдем из начальных условий (2.6). И, окончательно, получим:

            (2.10)

Примем для простоты, что в момент броска мяч находится в начале координат и на одном уровне с корзиной (т.е. 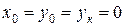). Под дальностью броска  будем понимать расстояние вдоль оси Ох, которое пролетит мяч от точки броска до пересечения с горизонтальной плоскостью, проходящей через кольцо корзины. Из соотношений (2.10) дальность броска выразится следующим образом:

.                                      (2.11)

С учетом (2.7) точность броска

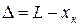.                                            (2.12)

Например, при броске мяча со штрафной линии можно принять следующие исходные данны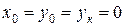е: ;  м; , Тогда из (2.11) и (2.12) получаем  м; м, т.е. бросок абсолютно точный.

Алгоритмическое решение задачи баскетболиста

Для численного решения задачи (системы дифференциальных уравнений) можно использовать метод Эйлера. Псевдокод алгоритма решения задачи баскетболиста имеет следующий вид:

1. Задать исходные данные задачи: массу мяча и т.д.

2. Выбрать шаг по времени Согласно методу Эйлера, изменять компоненты скорости мяча по формулам: , а координаты – по формулам: .

3. Остановить итерационный процесс при достижении условий (2.8).

Отметим, что при равной начальной высоте мяча и высоте кольца, для остановки итерационного процесса достаточно проверять условие , так как это будет означать, что мяч летит выше кольца.

Программную реализацию алгоритмической модели можно осуществить  в системе Mathcad. (кто хочет получить бонус к экзамену, можете сделать.)

Для тестирования программы целесообразно использовать результаты вычислений, полученные в предыдущем пункте по аналитической модели.

Проверка адекватности модели

Под адекватностью математической модели будет пониматься степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.

Проверка адекватности модели преследует две цели:

1) убедиться в справедливости совокупности гипотез, сформулированных на этапах концептуальной и математической постановок. Переходить к проверке гипотез следует лишь после проверки использованных методов решения, комплексной отладки и устранения всех ошибок и конфликтов, связанных с программным обеспечением;

2) установить, что точность полученных результатов соответствует точности, оговоренной в техническом задании.

Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных, ранее и хо­рошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором — о сравне­нии с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требо­ваний, предъявляемых к модели, и ее назначения. При этом долж­на учитываться точность получения экспериментальных результа­тов или особенности постановок тестовых задач. В моделях, пред­назначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается погрешность до 10-15%. В моделях, исполь­зуемых в управляющих и контролирующих системах, допустимая погрешность должна быть не более 1—2% и даже меньше. Как правило, различают качественное и количественное совпа­дение результатов сравнения. При качественном сравнении требуется лишь совпадение некоторых характерных особенностей в распределении исследуемых параметров (например, наличие экстремальных точек, положительное или отрицательное значение параметра, его возрастание или убывание и т.д.). Фактически при качественном сравнении оценивается совпадение лишь вида функции распределения параметров (убывающая или возрастающая, с одним экстремумом или с несколькими). Вопрос о количественном сравнении можно ставить лишь после удовлетворительного ответа на вопрос о качественном соответствии результатов. При количественном сравнении большое значение следует придавать точности исходных данных для моделирования и соответствующих им значений сравниваемых параметров.

Неадекватность результатов моделирования возможна, по крайней мере, по трем причинам:

1) значения задаваемых параметров модели не соответствуют допустимой области этих параметров, определяемой принятой системой гипотез. Например, в задаче баскетболиста гипотезу об отсутствии сопротивления воздуха можно использовать лишь при относительно малых (менее 5 м/с) скоростях движения тела. При больших значениях начальной скорости мяча влияние силы сопротивления будет существенным;

2) принятая система гипотез верна, но константы и параметры в использованных определяющих соотношениях установлены не точно. Например, в случае задачи баскетболиста значение ускорения свободного падения g может быть уточнено в зависимости от широты местности, где находится баскетболист;

3) неверна исходная совокупность гипотез.

Все три случая требуют дополнительного исследования как моделируемого объекта (с целью накопления новой дополнительной информации о его поведении), так и исследования самой модели (с целью уточнения границ ее применимости).

Отметим, что в данном случае не анализируется влияние выбранного численного метода на точность получаемого решения, а значит и на адекватность модели. Однако, используемый численный метод решения задачи может оказаться несостоятельным.

Соотношения (2.10) являются аналитическим решением задачи баскетболиста и позволяют определить значения координат и скоростей центра масс мяча в любой момент времени. Для координат х и у соотношения (2.10) есть уравнения параболы в параметрической форме. Мяч при броске движется по траектории, близкой к параболе. Поэтому в данном случае можно гово говорить о качественном совпадении результатов моделирования и экспериментальных данных. Вопрос о количественном совпадении результатов моделирования и эксперимента скорее всего будет решен отрицательно, так как отказ от учета силы сопротивления воздуха является грубым предположением. Для удовлетворительной оценки точности попадания мяча в корзину расхождение результатов моделирования и эксперимента не должно превышать 1—2 см. Поэтому гипотезу об отсутствии силы сопротивления воздуха в концептуальной постановке задачи заменим новой: сила сопротивления воздуха прямо пропорциональна скорости мяча:

,

где  - коэффициент сопротивления, зависящий от свойств среды и формы тела.

Для тела в форме шара коэффициент сопротивления определялся по формуле Стокса:

,

 - динамическая вязкость среды (для воздуха при температуре 20°С и давлении 1 атм = 0,0182 Н с/м²).

В соответствии с принятыми в баскетболе правилами длина окружности мяча может изменяться от 0,749 до 0,780 м, что соответствует изменению радиуса мяча от 0,119 до 0,124 м. Масса мяча должна быть в пределах от 0,567 до 0,650 кг. Примем для определенности радиус мяча R =0,12 м, а массу мяча m = 0,6 кг. Тогда коэффициент сопротивления среды составляет 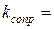 0,0412 Нс/м.

Соотношения (2.5) в математической постановке задачи следует заменить на новые:

Разделяя переменные и интегрируя с учетом начальных условий (2.6), можно получить решение в следующем виде:

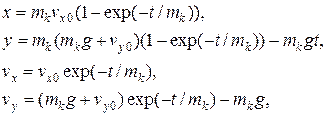              (2.13)

где .

Для определения дальности броска следует второе соотношение в (2.13) записать в виде

,

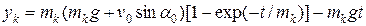где 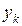- координата центра корзины. При  получим нелинейное уравнение относительно времени:

.            (2.14)

Определив время из решения (2.14) и подставив его в первое из соотношений (2.13), можно найти дальность броска. Однако в данном случае нет возможности определить аналитическое решение соотношения (2.14), что не позволяет построить соотношение для дальности L броска, аналогичное (2.11). В этом случае можно только сравнить результаты решения (2.10) и (2.13) для некоторых фиксированных значений и .

Сила сопротивления воздуха зависит не только от , но и от скорости мяча. Ниже приведены данные сравнения силы сопротивления по отношению к силе тяжести.

м/с	5	10	15	20
, Нс/м2	0,206	0,412	0,618	0,824
, %	3,5	7,0	10,5	14,0

 

Как можно видеть, сила сопротивления воздуха при скорости движения мяча 20 м/с не превышает 14% величины силы тяжести. Однако даже такое незначительное воздействие на движение мяча может существенно сказаться на точности броска. Так, при броске мяча под углом 45° с начальной скоростью 6,44 м/с дальность броска с учетом и без учета сил сопротивления будет отличаться на 17 см. При радиусе корзины R_к = 23,3 см разница составляет более половины R_к.

Учет сил сопротивления приводит к изменению решения задачи. Так, при моделировании без учета сопротивления среды броска мяча со штрафной линии при начальных данных 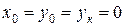,  4,225 м, 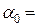 45° полученный в п. 2.4 результат для начальной скорости составил 6,44 м/с. С учетом сопротивления среды начальная скорость мяча должна быть равной 6,575 м/с, т.е. увеличится на 2,1%.