Рассмотрим множество  бесконечно дифференцируемых функций
бесконечно дифференцируемых функций 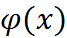 , которые обращаются в нуль вне некоторого отрезка, своего для каждой функции (финитные функции). Сходимость последовательности функций
, которые обращаются в нуль вне некоторого отрезка, своего для каждой функции (финитные функции). Сходимость последовательности функций  к функции
к функции 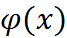 определим следующим образом:
определим следующим образом:
1) 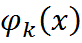 обращаются в нуль вне некоторого отрезка, общего для всех функций,
обращаются в нуль вне некоторого отрезка, общего для всех функций,
2) для каждого  последовательность
последовательность  равномерно сходится к
равномерно сходится к 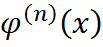 ,
,

Множество финитных бесконечно дифференцируемых функций с так определенной сходимостью называется пространством основных функций.
Пространство обобщенных функций.
Линейные непрерывные функционалы на пространстве основных функций 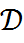 называются обобщенными функциями
называются обобщенными функциями  Их действие на основную функцию
Их действие на основную функцию  будем обозначать так:
будем обозначать так:

Сходимость последовательности обобщенных функций  к обобщенной функции
к обобщенной функции 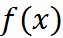 определим следующим образом:
определим следующим образом:
для каждой основной функции 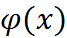 числовая последовательность
числовая последовательность  сходится к числу
сходится к числу  ,
,

Множество линейных непрерывных функционалов на пространстве финитных бесконечно дифференцируемых функций с так определенной сходимостью называется пространством обобщенных функций  (распределений Шварца).
(распределений Шварца).
Примеры.
1) Пусть  обычная локально интегрируемая функция (интегрируемая по любому конечному промежутку). Тогда она порождает функционал – обобщенную функцию, которая действует на основные функции по правилу:
обычная локально интегрируемая функция (интегрируемая по любому конечному промежутку). Тогда она порождает функционал – обобщенную функцию, которая действует на основные функции по правилу:

где интеграл на самом деле берется по конечному промежутку, т.к. 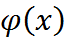 обращается в нуль вне некоторого отрезка. Такие обобщенные функции называются регулярными. Остальные обобщенные функции называются сингулярными.
обращается в нуль вне некоторого отрезка. Такие обобщенные функции называются регулярными. Остальные обобщенные функции называются сингулярными.
2) Дельта – функция Дирака:
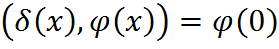
и сдвинутая дельта – функция Дирака:

Можно показать, что дельта – функция Дирака – сингулярная обобщенная функция.
Дельта – функцию Дирака можно продолжить с пространства 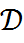 на пространство непрерывных функций, т.е. функционал
на пространство непрерывных функций, т.е. функционал
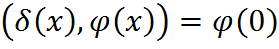
определен для любой непрерывной функции 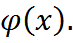
 2020-06-12
2020-06-12 252
252








