Рассмотрим сначала регулярные обобщенные функции. Пусть 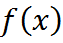 дифференцируемая функция. Тогда
дифференцируемая функция. Тогда
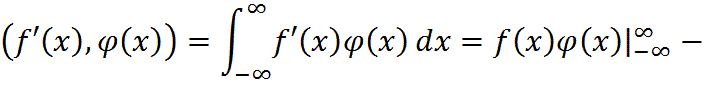
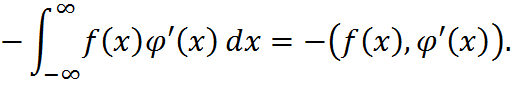
Это равенство примем за определение поризводной любой обобщенной функции:
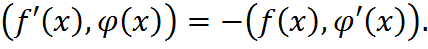
Поскольку основные функции 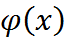 бесконечно дифференцируемы, то обобщенные функции имеют производные любого порядка:
бесконечно дифференцируемы, то обобщенные функции имеют производные любого порядка:
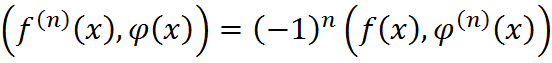
Примеры.
1) Производная дельта-функции.
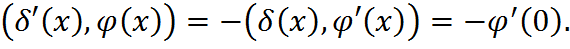
Производную дельта-функции можно продолжить с пространства 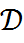 на пространство непрерывно дифференцируемых функций, т.е. функционал
на пространство непрерывно дифференцируемых функций, т.е. функционал
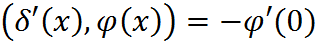
определен для любой непрерывно дифференцируемой функции 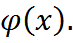
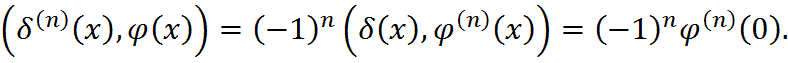
Производнуюго 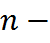 го порядка дельта-функции можно продолжить с пространства
го порядка дельта-функции можно продолжить с пространства 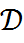 на пространство
на пространство 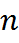 раз непрерывно дифференцируемых функций, т.е. функционал
раз непрерывно дифференцируемых функций, т.е. функционал
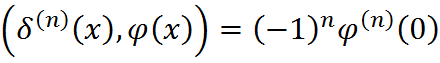
определен для любой 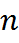 раз непрерывно дифференцируемой функции
раз непрерывно дифференцируемой функции 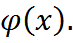
2) Производная функции Хевисайда.
Функция Хевисайда является регулярной обобщенной функцией и действует на основные функции по правилу:
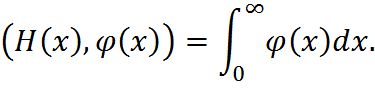
Ее производная
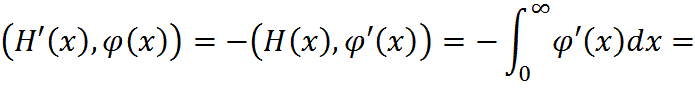
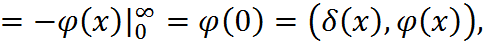
т.е.
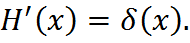
Преобразование Лапласа дельта-функции и ее производных.
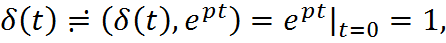
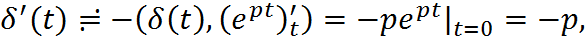
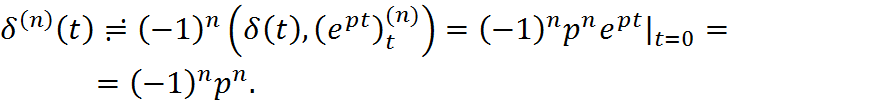
 2020-06-12
2020-06-12 194
194







