Степенные ряды. Радиус сходимости.
Пример 1. 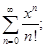 Для этого ряда
Для этого ряда 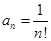 и
и 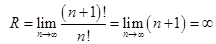 . Ряд абсолютно сходится на всей числовой прямой.
. Ряд абсолютно сходится на всей числовой прямой.
Пример 2. 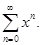 Здесь
Здесь 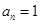 и
и  . В точках
. В точках 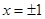 ряд, очевидно, расходится.
ряд, очевидно, расходится.
Пример 3. 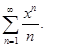 Для этого ряда
Для этого ряда 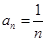 и
и 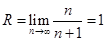 . В точке
. В точке 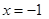 числовой ряд
числовой ряд 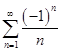 сходится по теореме Лейбница. В точке
сходится по теореме Лейбница. В точке 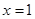 гармонический ряд
гармонический ряд 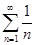 расходится.
расходится.
Пример 4. 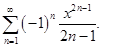 Здесь
Здесь 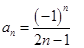 для нечетных номеров и
для нечетных номеров и 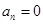 - для четных. Поэтому
- для четных. Поэтому 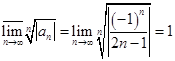 и
и 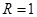 . В точках
. В точках 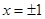 получается условно сходящийся ряд
получается условно сходящийся ряд 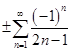 .
.
Пример 5. 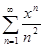 . Здесь
. Здесь 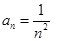 и
и 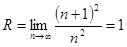 . В точках
. В точках 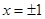 имеем ряд
имеем ряд 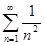 , который абсолютно сходится.
, который абсолютно сходится.
Разложение элементарных функций в степенные ряды
Разложение 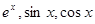 .
.
Для получения разложения 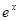 заметим, что
заметим, что 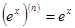 , и для любого отрезка мы получаем:
, и для любого отрезка мы получаем: 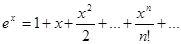 . Данный ряд сходится на всей числовой оси.
. Данный ряд сходится на всей числовой оси.
Для получения разложения 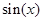 заметим, что
заметим, что 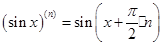 , для разложения
, для разложения 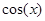 производная любого порядка может быть вычислена по формуле
производная любого порядка может быть вычислена по формуле 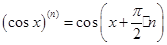
Поэтому 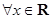
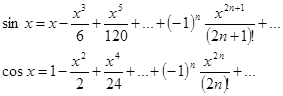
Разложение 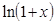 .
.
Используем равенство: 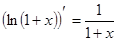 . Представляя функцию
. Представляя функцию 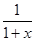 как сумму бесконечной убывающей прогрессии со знаменателем
как сумму бесконечной убывающей прогрессии со знаменателем 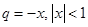 :
: 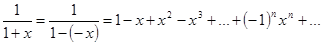 . Интегрируя это разложение в пределах от 0 до
. Интегрируя это разложение в пределах от 0 до 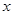 , получим:
, получим: 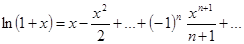 . Это равенство справедливо при
. Это равенство справедливо при 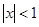 . Кроме того, т.к. ряд
. Кроме того, т.к. ряд 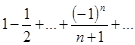 сходится по теореме Лейбница, равенство сохранится и при
сходится по теореме Лейбница, равенство сохранится и при 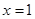 .
.
Разложение 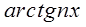 .
.
Используем равенство: 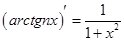 . Далее, как и выше, при
. Далее, как и выше, при 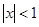
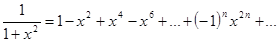 . Поэтому, при
. Поэтому, при 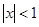
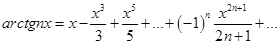 . Кроме того, ряд
. Кроме того, ряд 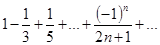 сходится. Значит, написанное выше разложение имеет место и при
сходится. Значит, написанное выше разложение имеет место и при 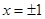 .
.
Разложение бинома 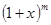 .
.
Если обозначить 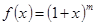 , то
, то 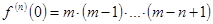 . Поэтому
. Поэтому 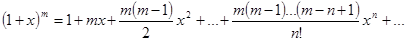 . Это разложение верно для всех
. Это разложение верно для всех 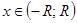 , где
, где 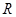 - радиус сходимости. Для нахождения
- радиус сходимости. Для нахождения 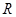 используем формулу
используем формулу 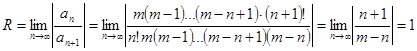 . Кроме того, без доказательства, отметим, что при
. Кроме того, без доказательства, отметим, что при 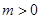 разложение справедливо и при
разложение справедливо и при 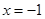 , а при
, а при 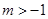 - для
- для 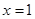 .
.
В заключение приведем несколько полезных следствий из разложения 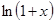 .
.
Следствие 1. Легко видеть, 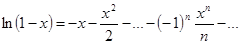 . Поэтому
. Поэтому 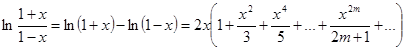 при
при 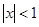 . Полагая
. Полагая 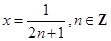 , получаем, что
, получаем, что 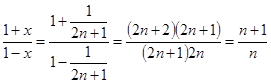 и
и 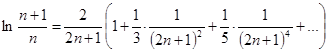 . Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.
. Этим разложением можно воспользоваться при вычислении логарифмов и при доказательстве формулы Стирлинга.
Следствие 2. Формула Стирлинга.
Приведем эту формулу без доказательства. 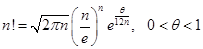
Пример 6. Найти область сходимости степенного ряда 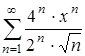 .
.
Решение. Радиус сходимости степенного ряда определяется по формуле:
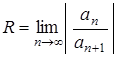 .
.
Так как
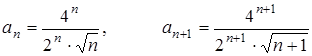 ,
,
то
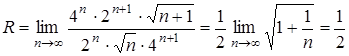 .
.
Степенной ряд сходится абсолютно в интервале 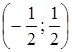 .
.
Исследуем поведение ряда на концах интервала.
При 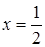 имеем
имеем 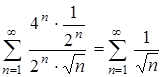 , данный ряд расходится.
, данный ряд расходится.
При 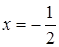 имеем
имеем 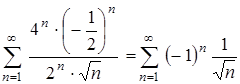 , ряд сходится по признаку Лейбница, причем сходится условно. Следовательно, область сходимости
, ряд сходится по признаку Лейбница, причем сходится условно. Следовательно, область сходимости
ряда является полуинтервал 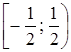 .
.
Пример 7. Вычислить 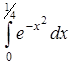 с точностью до
с точностью до 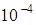 .
.
Решение. Разложение подынтегральной функции в степенной ряд имеет вид:
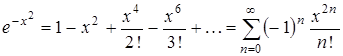 .
.
Интегрируя этот ряд почленно, получим
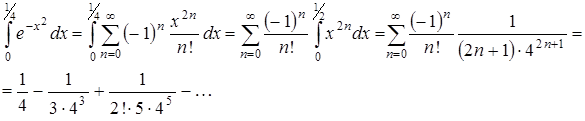
Полученный числовой ряд есть ряд Лейбница. Погрешность происходящая от отбрасывания всех членов начиная с третьего, будет по абсолютной величине меньше третьего члена:
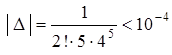 .
.
Вычисляя с точностью до 0,0001, найдем
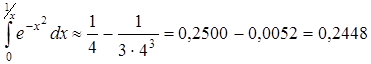
 2020-06-12
2020-06-12 520
520







