Если  является функцией периодической, то естественно раскладывать ее в функциональный ряд также по периодическим функциям, например, по косинусам и синусам.
является функцией периодической, то естественно раскладывать ее в функциональный ряд также по периодическим функциям, например, по косинусам и синусам.
О п р е д е л е н и е
Тригонометрическим рядом называется функциональный ряд вида:
 (1)
(1)
или, в более общем виде, ряд:
 , (2)
, (2)
где  – постоянное число, а постоянные числа
– постоянное число, а постоянные числа 
 называются коэффициентами тригонометрического ряда.
называются коэффициентами тригонометрического ряда.
КОЭФФИЦИЕНТЫ ФУРЬЕ ФУНКЦИИ
На основе условий ортогональности Фурье получил формулы коэффициентов тригонометрического ряда (1), соответствующего функции  :
:
 ; (3)
; (3)
 ,
,  ; (4)
; (4)
 ,
,  . (5)
. (5)
Общие формулы коэффициентов Фурье  -периодической функции
-периодической функции  :
:
 ; (6)
; (6)
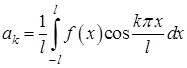 ,
,  ; (7)
; (7)
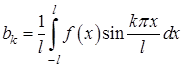 ,
,  . (8)
. (8)
Пример 1
Разложить в ряд Фурье функцию периода  , заданную на интервале
, заданную на интервале  формулой:
формулой:  (рис. 1).
(рис. 1).
 |
y
-4π -3p -2p -p 0 p 2p 3p 4π x
Рис. 1
Решение. Эта функция удовлетворяет условиям Дирихле и, следовательно, может быть разложена в ряд Фурье. Найдем коэффициенты Фурье  :
:

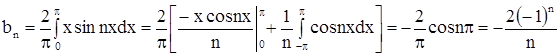 ,
,
0
т.к. 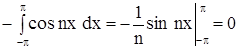 .
.
Следовательно, ряд Фурье функции  будет иметь вид
будет иметь вид
 .
.
Так как функция  удовлетворяет условиям Дирихле, то в любой точке непрерывности
удовлетворяет условиям Дирихле, то в любой точке непрерывности  сумма ряда равна значению функции. В точках
сумма ряда равна значению функции. В точках  и
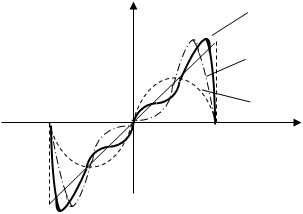
и  сумма ряда равна нулю. На рис. 2 показаны графики: функции
сумма ряда равна нулю. На рис. 2 показаны графики: функции  и частичных сумм ряда, содержащие 1, 2 и 3 члена. Из рисунка видно, как график частичных сумм ряда приближается к графику функции
и частичных сумм ряда, содержащие 1, 2 и 3 члена. Из рисунка видно, как график частичных сумм ряда приближается к графику функции  при увеличении членов суммы.
при увеличении членов суммы.
 y
y 


Пример 2. Разложить в ряд Фурье периодическую функцию, заданную на интервале – периоде.

Решение. Функция f (x) удовлетворяет условию Дирихле, поэтому раскладывается в ряд Фурье.
 .
.
Вычисляя коэффициенты Фурье функции f (x):
 ,
,
 ,
,

так как
 ,
,
 .
.
 .
.
 2020-06-12
2020-06-12 149
149







