Определение площади необходимого для изготовления материала для абажура. (Расчет площади боковой поверхности конуса)

Тема: Формулы объема и площади поверхностей усечённых пирамиды и конуса.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава VII, § 3, п. 80-81), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.

Теоретический минимум и задачи

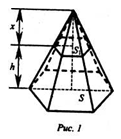
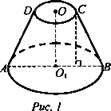
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис. 1).

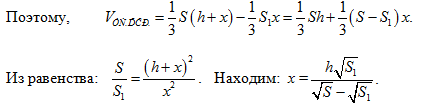
Подставим это выражение для х в первую формулу,

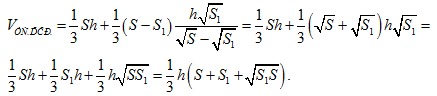
Объем усеченного конуса

Усеченный конус можно получить, вращая прямоугольную трапецию 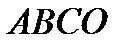 вокруг оси .

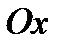Найдем уравнение прямой 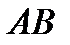, образующей коническую поверхность. Для этого положим 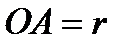, , 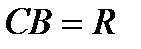 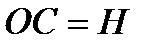и напишем уравнение в виде , , .

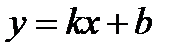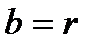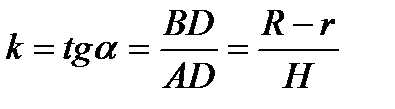Таким образом, искомое уравнение будет: .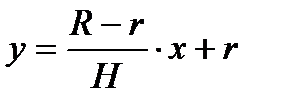

Согласно формуле 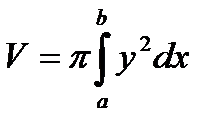, найдем: .

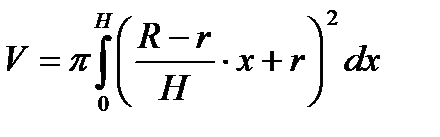Вычислим определенный интеграл способом подстановки. Положим 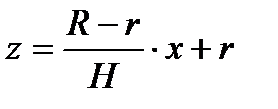. Тогда 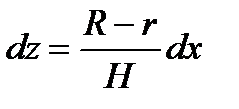. Отсюда 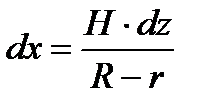. Новыми пределами интеграла будут: , .

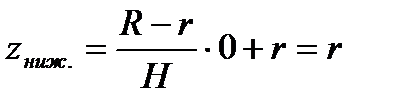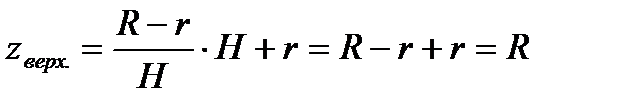Следовательно,

.

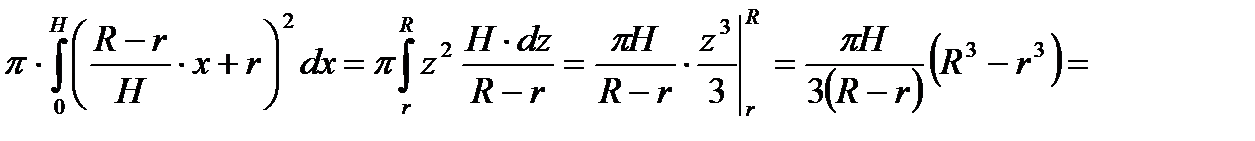
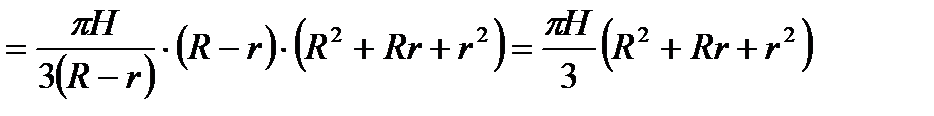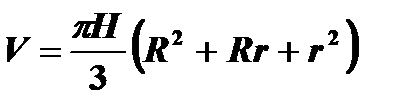
Площадь боковой поверхности правильной усечённой пирамиды: S_бок.= (P₁+P₂)⋅h, где P₁и P₂−периметры оснований.

Площадь боковой поверхности усеченного конуса.

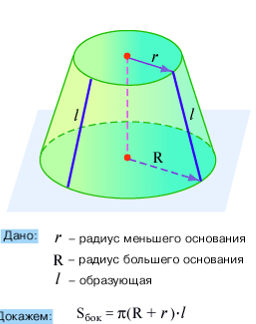
Рассмотрим решение задач.

Задача 1

Определение площади необходимого для изготовления материала для абажура. (Расчет площади боковой поверхности конуса).

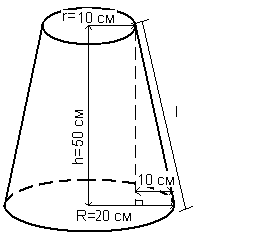Абажур имеет форму усеченного конуса. Высота абажура равна 50 см, нижний и верхний диаметры - 40 и 20 см соответственно.

Определить с точностью до 3х значащих цифр площадь материала, необходимого для изготовления абажура.

Как было определено выше, площадь боковой поверхности усеченного конуса S=π l(R+r).

Поскольку верхний и нижний диаметры усеченного конуса равны 40 и 20 см, то из рис. находим r=10 см, R=20 см и

l=(50 ²+10²)^1/2=50,99 согласно теореме Пифагора,

Следовательно, площадь боковой поверхности конуса равна S=π 50,99(20+10)=4803,258 см², т.е. площадь необходимого для изготовления абажура материала равняется 4800 см² с точностью до 3х значащих цифр, хотя, конечно, сколько на самом деле уйдет материала зависит от кроя.

Задача № 2 Объем усеченной пирамиды равен 210 см³, площадь нижнего основания 36 см², верхнего 9 см². Найдите высоту пирамиды.

Решение:

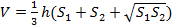, 210= 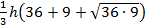, h=10 см

Задача № 708. Радиусы оснований усеченного конуса равны 3 м и 6 м, а образующая равна 5 м. Найдите объем конуса.

Дано: усеченный конус, r = О₁С = 3 м, ОВ = R = 6 м, СB = 5 м (рис. 1).

Найти: Vус.п.

С1

Решение: 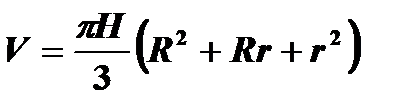  Проведем СС₁ ⊥ АВ, O₁С = OС₁ = 3 м, C₁B = 6 - 3 = 3 (м). Из ΔСВС₁ (∠C1 = 90°) по теореме Пифагора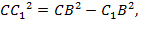 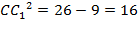, 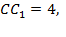V= 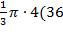+9+18)=84π м³.