Типы соединений элементов

Множества элементов называются соединениями.

Различают три типа соединений:

· перестановки из n элементов;

· размещения из n элементов по m;

· сочетания из n элементов по m (m < n).

4.1 Перестановки.

На практике часто возникают задачи, связанные с установлением порядка во множестве. Например, число мест равно количеству людей, на которых мы должны разместить их. Такая ситуация встречается часто – рассадить n человек на n мест, или приписать каждому человеку номер. Первый человек может выбрать любое из n мест, второй человек выбирает из (n - 1) оставшихся мест, третий человек может выбрать из уже (n - 2) мест, …, предпоследний человек выбирает из 2 мест, последний человек получает последнее место. Мы получаем произведение всех целых чисел от n до 1.

В общем виде произведение всех целых чисел от 1 до n включительно обозначают

n! = 1·2·3…(n – 2) · (n – 1) · n.

Установленный в конечном множестве порядок называют перестановкой его элементов.

Определение: Перестановкой из n элементов называется любое упорядоченное множество из n элементов.

Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте.

Перестановки можно образовывать из элементов любого конечного множества. Число перестановок из n элементов обозначают Р_n. Возьмем одноэлементное множество { a }. Один элемент можно упорядочить единственным образом, следовательно, Р₁ = 1.

Перестановки – это такие соединения по n элементам из данных элементов, которые отличаются одно от другого порядком элементов.

Возьмем двух элементное множество { a, b }. В нем можно установить два порядка: { a, b } или { b, a }. Следовательно, число перестановок из двух элементов Р₂ = 2.

Три буквы во множестве { a, b, c } можно расположить, по порядку шестью способами: { a, b, c }{ a, c, b }{ b, a, c }{ b, c, a }{ c, b, a }{ c, a, b }.

Следовательно, общее число способов упорядочения трех элементов множества

Р₃ = 3 · Р₂ = 3 · 2 · 1 = 6.

Р_n = n · (n - 1) · (n – 2) · … · 2 · 1 = n!

Определение: Пусть n - натуральное число. Через n! (читается "эн факториал") обозначается число, равное произведению всех натуральных чисел 1 от до n:

n! = 1 · 2 · 3 ·... · n.

В случае, если n = 0, по определению полагается: 0! = 1.

Пример № 6  Найдем значения следующих выражений: 1! = 1;    2! = 1 · 2 = 2;    3! = 1 · 2 · 3 = 6

Пример № 7  Чему равно а) Р ₅; б) Р _3.

Р_n = n! = n · (n - 1) · (n – 2) · … · 2 · 1;

Р ₅=5! = 5*4*3*2*1= 120; Р ₃=3! = 1*2*3 = 6

Пример № 8  Упростите

а) 7! *8 = 8!             б) 12!*13*14 = 14!            в) κ!*(κ + 1) = (κ + 1)!

Пример № 9   Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках? n =8       Р ₈=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320

Размещения.

Размещениями из m элементов по n элементов (n ≤ m) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.

Определение. Размещением из n элементов по m называется любое упорядоченное множество из m элементов, состоящее из элементов n элементного множества.

Число размещений из m элементов по n обозначают 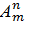 (от французского «arrangement» - «размещение») и вычисляют по формуле:

Пример № 9 Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?

Решение. Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (урока) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре, то есть A ₉⁴:

  

Пример № 10 Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты?

Решение. Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A ₂₄²:

  

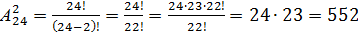
Сочетания.

Сочетаниями из m элементов по n элементов (n ≤ m) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.

Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества

Число сочетаний из n элементов по m обозначают (от французского «combination» - «сочетание») и вычисляют по формуле:

Пример № 11     Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных?

n =24, m =2