Математическое ожидание непрерывной случайной величины 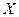 вычисляется по формуле:
вычисляется по формуле: 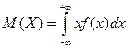 ; (10)
; (10)
дисперсия 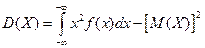 или (11)
или (11)

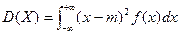 . (12)
. (12)
Пример 7. Найдите математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины 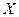 , заданной функцией распределения
, заданной функцией распределения 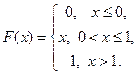
Решение. Найдем плотность распределения:
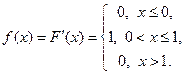
Математическое ожидание: 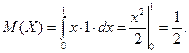
Среднее арифметическое.
Дисперсия 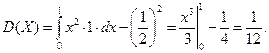
Следовательно, среднее квадратическое отклонение равно: 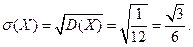
Пример 8. Плотность вероятности случайной величины имеет вид:
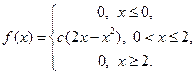
Найдите: 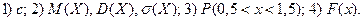
Решение. 1) По основному условию нормировки 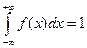 . Тогда получаем:
. Тогда получаем: 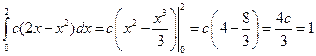 . Откуда
. Откуда 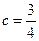 .
.
2) По формуле математического ожидания находим:
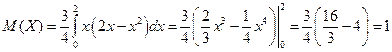 .
.
Дисперсия случайной величины равна: 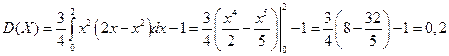 .
.
Следовательно, среднее квадратическое отклонение равно: 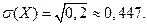
3) 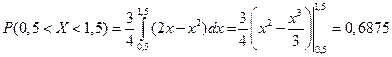 .
.
4) 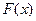 и
и 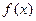 связаны формулой
связаны формулой 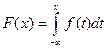 .
.
Поэтому, при 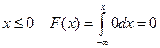 .
.
При 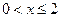
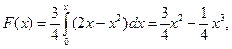
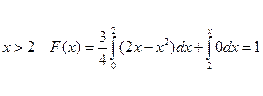 .
.
Следовательно, 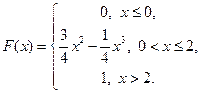
 2020-06-08
2020-06-08 123
123







