Любой вектор в пространстве можно разложить по трем заданным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство.
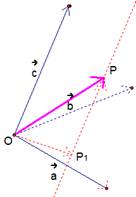
Рис. 5. Разложение вектора по трем некомпланарным
Дано: некомпланарные векторы 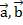 и
и 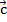 , произвольный вектор
, произвольный вектор 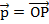 .
.
Построим все заданные векторы из одной точки – точки О (рис. 5). Рассмотрим плоскость, образованную векторами 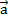 и
и 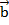 . Из точки Р проведем прямую
. Из точки Р проведем прямую 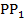 , параллельно направлению
, параллельно направлению 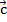 .
. 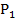 – точка пересечения плоскости и прямой. Векторы
– точка пересечения плоскости и прямой. Векторы 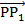 и
и 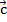 по построению коллинеарны, значит имеем:
по построению коллинеарны, значит имеем: 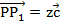 . Теперь, согласно правилу треугольника, имеем:
. Теперь, согласно правилу треугольника, имеем: 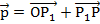 . Вектор
. Вектор 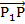 мы нашли. Вектор
мы нашли. Вектор 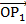 , согласно построению, лежит в плоскости векторов
, согласно построению, лежит в плоскости векторов 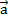 и
и 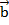 , значит, согласно теореме, рассмотренной выше, о разложении вектора через два неколлинеарных имеем:
, значит, согласно теореме, рассмотренной выше, о разложении вектора через два неколлинеарных имеем: 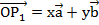 .
.
Так, получено разложение произвольного вектора в пространстве через три некомпланарных вектора: 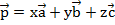
Докажем, что такое разложение единственно. Используем метод от противного. Предположим, что есть еще тройка чисел (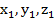 ), с помощью которой можно заданный вектор разложить по трем некомпланарным.
), с помощью которой можно заданный вектор разложить по трем некомпланарным. 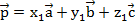 . Имеем систему:
. Имеем систему:

Вычтем из первого уравнения второе:
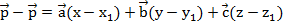
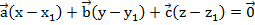
Получить нулевой вектор из трех некомпланарных ненулевых векторов путем их сложения можно только в случае, когда: 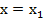 ,
, 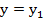 ,
, 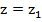 .
.
Так, доказано, что возможно единственное разложение вектора по трем некомпланарным.
Домашнее задание
1. в параллелепипеде 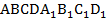 точка М принадлежит ребру AD, причем АМ:MD=1:3. Точка Р принадлежит ребру DC,
точка М принадлежит ребру AD, причем АМ:MD=1:3. Точка Р принадлежит ребру DC, 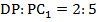 . Разложите вектор
. Разложите вектор 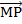 по векторам
по векторам 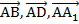
 2020-06-08
2020-06-08 990
990







