Теорема о компланарных векторах, сложение векторов в пространстве

Математика

Класс

Урок 15 - 16

Компланарные векторы

Введение, понятие компланарности векторов

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Рассмотрим векторы 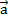и 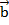: рис. 1

Рис. 1. Векторы 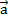и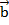

Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам: рис. 2, 3.

Рис. 2. Векторы на плоскости

Теорема о разложении вектора по двум неколлинеарным

Рис. 3. Разложение вектора через два неколлинеарных

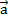Данный факт легко доказывается. Пусть . Из точки С проводим прямую CB, параллельно вектору . Получаем вектор , коллинеарный вектору 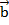. Аналогично из точки С проводим прямую CА, параллельно вектору 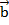. Получаем вектор , коллинеарный вектору 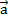. Это означает, что существуют такие два числа х и у, причем единственные, что:

Напомним, что коллинеарными называются векторы, принадлежащие одной и той же или параллельным прямым.

Теорема о компланарных векторах, сложение векторов в пространстве

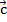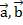Если вектор можно представить в виде , где х и у – конкретные числа, то вектора и 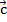компланарны.

Рис. 4. Сложение векторов в пространстве

Рассмотрим три вектора 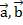и 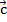в пространстве. На плоскости мы строили параллелограмм на двух заданных векторах. В пространстве же мы можем построить параллелепипед на трех заданных векторах. Найдем сумму этих векторов (рис. 4).

Из точки К откладываем заданные векторы. Достраиваем параллелепипед. Суммой трех заданных векторов будет диагональ параллелепипеда:

Данный факт легко доказать с помощью правила многоугольника. Согласно свойствам параллелепипеда, имеем пары равных векторов: , . Так, получаем: , ч.т.д.

Если заданы три некомпланарных вектора, то мы можем разложить любой заданный четвертый вектор через три заданных. Например, заданы некомпланарные векторы 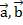и 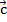. Тогда любой вектор можно представить в виде суммы: , где х, у и z – конкретные числа, причем для заданного вектора единственные. Эти числа называются коэффициентами разложения.