Тема: Объем и его измерение. Интегральная формула объема.
Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава VII, § 1, п. 74, глава VII, § 3, п. 78), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.
Теоретический минимум и задачи
Понятие объема тела
Еще в глубокой древности у людей возникла необходимость в измерении количества различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определенной вместимости, т.е. определяя их количество по объему. Понятие объема в стереометрии вводится аналогично понятию площади в планиметрии. В планиметрии мы определяли площадь так: площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Сформулировать аналогично данному понятию понятие объема. Величина части пространства, занимаемого геометрическим телом, называется объемом этого тела.
Единицы измерения объема
В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел.
Среди них английские меры:
· Бушель – 36,4 дм3
· Галлон – 4,5 дм3
· Баррель (сухой) – 115,628 дм3
· Баррель (нефтяной) – 158,988 дм3
· Английский баррель для сыпучих веществ 163,65 дм3.
В Киевской Руси существовала мера зерна – кадь. (Это примерно 230 кг ржи) Жидкости же мерили бочками и ведрами. В XIX в. система мер жидкости имела вид:
· Ведро – 12 дм3
· Бочка – 490 дм3
· Штоф – 1,23 дм3 = 10 чарок
· Чарка – 0,123 дм3=0,1 штофа = 2 шкалика
· Шкалик – 0,06 дм3 = 0,5 чарки.
Для того, чтобы определить какая из двух емкостей вместительнее, можно заполнить одну из них водой, а затем проверить, вся ли вода поместится в другую, и если вся, то заполнит ли она ее полностью. Однако решить эту задачу иначе – вычислить объем каждой емкости. Для этого нам нужны единицы объемов. Когда в планиметрии мы вводили единицы площади, то за единицу площади брали квадрат со стороной 1 см (1 см2).
Аналогично, за 1см3 принимаем куб с ребром 1 см. Процедура измерения объемов аналогична процедуре измерения площадей. Число измерения (единичных кубов) и частей единицы, содержащихся в данном теле, принимается за числовое значение объема при выбранной единице измерения. Это число может быть как рациональным (в частности, целым), так и иррациональным.
Свойства объемов
Объём тела определим с помощью свойств:
Равные тела имеют равные объемы. (Понятие определяется на основе понятия наложения).
Объем тела, состоящего из некоторых частей, равен сумме объемов этих частей.
3. Объем куба с ребром а равен а3.
4) Интегральная формула объёма
Введённое выше определение объёма хорошо использовать для нахождения объёмов многогранников, но как вычислить объёмы тел вращения или объем планеты, кометы, метеорита, и т.д.
Обратимся к истории. 1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер, очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы. Этот вопрос как раз входил в круг интересов Иоганна Кеплера, лишь недавно выпустившего труд “новая астрономия”. Так родилась его “Новая стереометрия винных бочек”, вышедшая в свет в 1615 году. Кеплер вычислял объёмы геометрических тел, основываясь на идее разложения тела на “тончайшие кружочки”, из этих частей составлял тело, объём которого ему уже известен.
Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
Вспомним, что называется определенным интегралом. Если функция f(x) непрерывна на промежутке I числовой оси, содержащей точки х=а и х=b, то разность значений F(b)-F(a) (где F(x) - первообразная f(x) на I) называется определенным интегралом от функции f(x) от a до b.
 При помощи определенного интеграла можно вычислить объем того или иного тела, используя формулу:
При помощи определенного интеграла можно вычислить объем того или иного тела, используя формулу:
Рассмотрим применение этой формулы для вычисления объёма тела.
№673. Задача: сечение тела плоскостью, перпендикулярной к оси  и проходящей через точку с абсциссой
и проходящей через точку с абсциссой 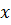 , является квадратом, сторона которого равна
, является квадратом, сторона которого равна  . Найти объем этого тела.
. Найти объем этого тела.
Решение: воспользуемся только что доказанной формулой.


По рисунку видно, что пределами интегрирования будут числа  . Поскольку сечение плоскости – квадрат, значит, площадь сечения равна
. Поскольку сечение плоскости – квадрат, значит, площадь сечения равна  .
.
Тогда получим, что объём этой фигуры равен 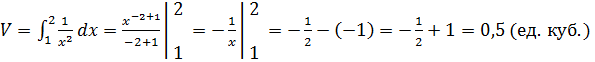 .
.
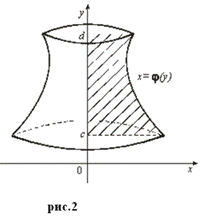
Напомним, что называется телом вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
 | |||
 | |||
Для тел вращения используется одна из формул
1.  , если вращение криволинейной трапеции вокруг оси ОХ.
, если вращение криволинейной трапеции вокруг оси ОХ.
2. 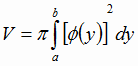 , если вращение криволинейной трапеции вокруг оси ОУ.
, если вращение криволинейной трапеции вокруг оси ОУ.
Рассмотрим примеры:
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.

Ответ: 1163 cm 3.
2. Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y =  , x = 4, y = 0.
, x = 4, y = 0.
Решение.

 2020-06-08
2020-06-08 1212
1212