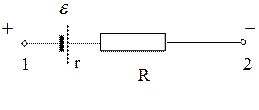 |
Участок цепи, содержащий (ЭДС)  и
и
электрическое сопротивление, называется
неоднородным. Напряжение 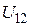 на таком участке равно:
на таком участке равно:
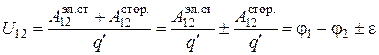 (3.15)
(3.15)
Для неоднородного участка цепи закон Ома имеет вид:
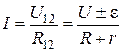 , (3.16)
, (3.16)
где 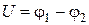 - разность потенциалов (напряжение) на концах участка;
- разность потенциалов (напряжение) на концах участка;  - электрическое сопротивление участка цепи;
- электрическое сопротивление участка цепи; 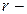 внутреннее сопротивление источника тока;
внутреннее сопротивление источника тока;  сопротивление проводника.
сопротивление проводника.
Знаки « » отражают тот факт, что сторонние силы могут совершать как положительную, так и отрицательную работу на рассматриваемом участке цепи.
» отражают тот факт, что сторонние силы могут совершать как положительную, так и отрицательную работу на рассматриваемом участке цепи.
Участок цепи, на котором не действуют сторонние силы, называется однородным
 Закон Ома для однородного участка цепи имеет вид:
Закон Ома для однородного участка цепи имеет вид:
 , (3.17)
, (3.17)
т.к. 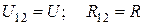 .
.
Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, 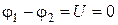 , и тогда закон Ома для такой цепи:
, и тогда закон Ома для такой цепи:

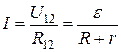 , (3.18)
, (3.18)
т.к.  .
.
При последовательном соединении проводников: 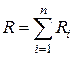 .
.
При параллельном соединении проводников: 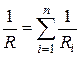 .
.
Единица электрического сопротивления в СИ:  Ом.
Ом.
Единица напряжения (ЭДС) в СИ: 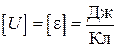 = В.
= В.
Закон Джоуля – Ленца
При прохождении тока по неподвижному проводнику, проводник нагревается. Количество выделившейся теплоты определяется законом Джоуля–Ленца. Для постоянного тока  оно равно
оно равно
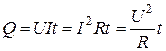 . (3.19)
. (3.19)
Элементарное количество теплоты
 .
.
Если 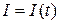 , или
, или  , то
, то
 . (3.20)
. (3.20)
Для элементарного цилиндра 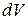 (см. закон Ома в дифференциальной форме), тепловая мощность на этом участке равна
(см. закон Ома в дифференциальной форме), тепловая мощность на этом участке равна
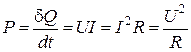 (3.21)
(3.21)
Удельная тепловая мощность
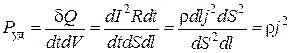 .
.
Используя закон Ома в дифференциальной форме: 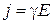 , получим
, получим
 . (3.22)
. (3.22)
(3.22) – закон Джоуля-Ленца в дифференциальной (локальной) форме.
Единица тепловой мощности в СИ: 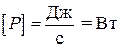 .
.
 2020-06-08
2020-06-08 110
110







