Тип точки
разрыва 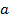
Определение
Пример
Устранимый
разрыв
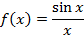
Неустранимый разрыв I рода
(разрыв с конечным скачком функции)
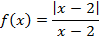
Неустранимый разрыв II рода
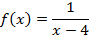
Пример 4. Найти такие числа 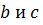 , при которых функция
, при которых функция
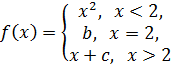
непрерывна в точке 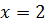 .
.
Решение:
1) _______________________________________________________________
__________________________________________________________________
2) Функция 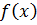 непрерывна в точке
непрерывна в точке 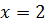 . если
. если
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Пример 5. Выяснить является ли непрерывной функция
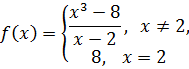
непрерывной в точке 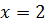 .
.
Решение:
1)_________________________________________________________________
2) ________________________________________________________________
3) ________________________________________________________________
Вывод: ____________________________________________________________
Приведем два примера:
Пример 1: Проследим, как ведут себя значения функции f(x) = 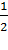 х 2 + 2, если значение аргумента х как угодно близко приближаются к числу 2.
х 2 + 2, если значение аргумента х как угодно близко приближаются к числу 2.
Обозначается х –˃2. Из рисунка следует, что если х –˃2 слева или справа, то соответствующие значения функции f(x) как угодно близко приближаются к числу 4, т.е. эти значения мало отличаются от числа 4.
В таком случае говорят, что функция f(x) =  х 2+ 2 имеет предел число 4 при х –˃2, или в точке х 0 = 2. Обозначается:
х 2+ 2 имеет предел число 4 при х –˃2, или в точке х 0 = 2. Обозначается: 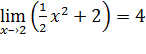
Пример 2: Проследим за значением функции 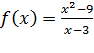 при х–˃3.
при х–˃3.
В отличие от предыдущего примера, в точке х0 = 3 функция не определена. Однако по графику нетрудно сделать вывод, что если х–˃3 (х ≠ 3), то соответствующие значения функции приближаются к числу 6 - предел функции при х–˃3, или в точке х0 = 3, т.е. 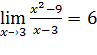 .
.
 2020-06-08
2020-06-08 99
99







