2020-06-08
112
Пример 1. Построить графики функций и ответить на вопросы.
1. Найдите односторонние пределы функции в точке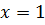 
.
2. Что можно сказать о наличии предела функции в точке ?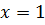
3. Укажите связь, которая существует между односторонними пределами функции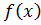 
и пределом этой функции в точке 
.
4. Что можно сказать о поведении графика в точке ?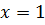
Определение 1. Функция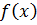 
, определенная в некоторой окрестности точки 
, называется непрерывной в точке , если _____________________(1)
Условия, которые должны выполняться для непрерывной в точке функции:
1) ________________________________________________________________
2) ________________________________________________________________
3) ________________________________________________________________
Определение 
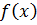. Функция , определенная в некоторой окрестности точки , называется непрерывной в точке , если _______________________
____________________________________________________________________________________________________________________________________
Пример 2. Используя определение 1, доказать непрерывность функции 
в точке .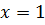
Решение:
1)________________________________________________________________
|
|
|
2) ________________________________________________________________
3) ________________________________________________________________
Вывод: ____________________________________________________________
Преобразуем равенство (1). _____________________________________
__________________________________________________________________
__________________________________________________________________
Разность 
называется приращением аргумента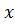 
в точке и обозначается 
, а разность f(x) — f(a) - приращением функции в точке , соответствующим приращению аргумента , и обозначается 
.
Определение 2. Функция называется непрерывной в точке , если
__________________________________________________________________
Пример 3. Используя определение 2, доказать непрерывность функции
при любом значении .
Решение:
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
По аналогии с понятием предела слева и предела справа вводится понятие непрерывности слева и непрерывности справа.
Определение 3. Функция 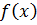определенная на полуинтервале 
называется непрерывной слева в точке , если________________ __________________________________________________________________
Определение 4. Функция 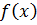определенная на полуинтервале 
называется непрерывной справа в точке , если ________________ _______________________________________________________________
Определение 5. Функция 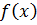называется непрерывной на интервале 
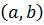, если ________________________________________________________
Определение 6. Функция называется непрерывной на отрезке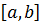 
, если __________________________________________________________
__________________________________________________________________
Свойства функций, непрерывных в точке
1) ________________________________________________________________
__________________________________________________________________
2) ________________________________________________________________
|
|
|
__________________________________________________________________
3) ________________________________________________________________
__________________________________________________________________
4) ________________________________________________________________
__________________________________________________________________
Свойства функций, непрерывных на отрезке
Теорема 1. _____________________________________________________
_______________________________________________________________
Теорема 2. _______________________________________________________
_______________________________________________________________
Теорема 3. ________________________________________________________
__________________________________________________________________
Теорема 4. ________________________________________________________
__________________________________________________________________
Определение 7. Точка называется точкой разрыва функции 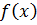, если в точке , __________________________________________________________________
__________________________________________________________________
