СЛАЙД 57. САРД в СК вентиляционного типа

Математическая модель объекта регулирования в САРД вентиляционного типа

При выводе дифференциального уравнения СК как объекта регулирования по давлению будем считать, что температура рабочей среды в СК являются величиной постоянной .

В переходном режиме изменение массы воздуха в СК характеризуется следующим уравнением:

, (1)

-расход газа на поддержание давления, расход газа через регулятор давления, расход газа при утечках

Выразим массу воздуха в СК на основании уравнения состояния газов через объем газа СК и давления:

(2)

где 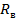- газовая постоянная воздуха.

Члены правой части уравнения (2) являются функциями нескольких переменных:

1. Подача воздуха в СК при через шланг с проходным сечением :

где - давление воздуха в пневмосистеме СК, - площадь проходного сечения шланга, по которому осуществляется наддув СК воздухом.

2. Сброс избыточного количества воздуха из СК через клапан регулятора давления:

- площадь открытия клапана сброса воздуха, - давление воздуха в кабине ЛА.

3. Количество воздуха, вытекающего из СК вследствие его негерметичности:

где - эквивалентная площадь отверстий утечки.

Динамические параметры СК как объекта регулирования по давлению определяются величиной частных производных, входящих в уравнение (2). Для аналитического определения величин частных производных можно воспользоваться известными формулами истечения воздуха через отверстия для двух случаев: докритического и закритического истечения.

СЛАЙД 58. При закритическом истечении подача и расход воздуха могут быть определены как (3):

, (3)

где

При докритическом истечении (4)

, , (4)

где .

СЛАЙД 59. Поскольку динамические свойства СК как объекта регулирования исследуются при малых изменениях регулируемого параметра, можно считать утечку воздуха постоянной в переходном режиме

Если предположить, что параметры , … в установившемся режиме имеют значения , , ,… а в переходном режиме получают малые приращения , то, разложив функции и в ряд Тейлора по приращениям до первой производной и подставив их в уравнение (2), получим (5)

(5)

После преобразования получим (6):

(6)

Тогда можно преобразовать уравнение к виду (7).:

(7)

где - возмущение, действующее на объект

СЛАЙД 60. Тогда получаем уравнение (8 )

(8)

Преобразуем в (9)

(9)

где - постоянная времени объекта регулирования (10)

(10)

Таким образом получили линейную модель САРД

Полученное уравнение в приращениях запишем в операторной форме: (11)

(11)

где – коэффициент эффективности регулятора расхода (12)

(12)

- возмущающее воздействие (13)

(13)

Изменение площади проходного сечения клапана 2, через которое происходит сброс избыточного воздуха из СК, пропорционально ходу клапан h (14):

(14)

, который в свою очередь, пропорционален прогибу анероидного сильфона, а следовательно, отклонению 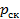от заданного (15):

(15)

СЛАЙД 61. Коэффициент пропорциональности для рассматриваемого случая оценивается как (16)

(16)

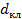– диаметр седла клапана расхода регулятора давления.

Уравнение движения клапана регулятора давления, установленного на выходе пневмосистемы (см рис 2.6) (17):

, (17)

Отсюда получаем уравнение 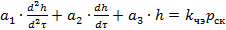(18)

(18)

Таким образом, математическая модель САРД давления рабочей среды СК вентиляционного типа определяется системой, состоящей из уравнения изменения давления рабочей среды в полости СК и уравнения изменения площади проходного сечения клапана расхода воздуха из СК (19)

(19)

Полученные математические модели и системы автоматического регулирования рабочей среды СК позволяют определить переходные характеристики.

Динамические параметры СК как объекта регулирования по давлению определяются величиной частных производных, входящих в уравнение (2.27). Для аналитического определения величин частных производных можно воспользоваться известными формулами истечения воздуха через отверстия для двух случаев (18) и (19):

(20)