Марковских процессов
Пример 3.1. Расчет надёжности системы при ненагруженном резервировании элементов.
В отличие от нагруженного резервирования (дублирования), при котором основной и резервный элемент работают одновременно, при ненагруженном резервировании работает только основной элемент, а резервный включается после его отказа.

Рис. 3.1. Схема ненагруженного резервирования
1 – основной элемент; 2 – резервный элемент; 3 – переключатель
Допустим, что основной и резервный элементы равнонадежны. Вероятность безотказной работы элемента:
 ,
,
где  ,
,  – средняя наработка до отказа, то есть распределение наработки до отказа описывается экспоненциальным законом.
– средняя наработка до отказа, то есть распределение наработки до отказа описывается экспоненциальным законом.
Рассмотрим функционирование системы, состоящей из основного и резервного элементов, с позиции теории марковских процессов [2].
Эта система в процессе функционирования может находиться в 3-х состояниях:
1. Работает основной элемент, резервный выключен.
2. Работает резервный элемент, основной отказал.
3. Отказали оба элемента.

Рис. 3.2. Граф переходов системы при ненагруженном резервировании элементов
Вероятность отказа одного элемента за время  равна
равна  . Поскольку рассматривается система без восстановления отказавших элементов, то после отказа резервного элемента система переходит в 3-е состояние, в котором остается с вероятностью, равной
. Поскольку рассматривается система без восстановления отказавших элементов, то после отказа резервного элемента система переходит в 3-е состояние, в котором остается с вероятностью, равной  . Такое состояние называется тупиковым, или поглощающим.
. Такое состояние называется тупиковым, или поглощающим.
Уравнения Колмогорова для рассматриваемой системы записываются в виде:

Раскрыв скобки, перенеся  в
в  -ом уравнении из правой части в левую, разделив обе части уравнения на
-ом уравнении из правой части в левую, разделив обе части уравнения на  и перейдя к пределу при
и перейдя к пределу при  , получаем следующую систему дифференциальных уравнений:
, получаем следующую систему дифференциальных уравнений:

Граф переходов рассматриваемой системы несвязный, так как попав в третье состояние система остается в нем и не может перейти ни в какое другое состояние, поэтому для определения вероятностей состояний необходимо решить систему дифференциальных уравнений.
Задавшись начальными условиями  ;
;  , решим систему дифференциальных уравнений операторным методом [3].
, решим систему дифференциальных уравнений операторным методом [3].
После преобразования Лапласа система дифференциальных уравнений превращается в систему алгебраических уравнений:

Из первого уравнения находим  , из второго уравнения
, из второго уравнения  .
.
По таблицам обратного преобразования Лапласа [3] находим оригиналы, соответствующие изображения  и
и 

 .
.
Так как система работоспособна, находясь в состоянии  или
или 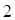 , то вероятность ее безотказной работы равна
, то вероятность ее безотказной работы равна 
 (3.1)
(3.1)
Интегрируя функцию  в пределах от
в пределах от 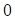 до
до  , находим среднюю наработку до отказа системы с ненагруженным резервированием элементов.
, находим среднюю наработку до отказа системы с ненагруженным резервированием элементов.
 .
.
Возьмем полученный интеграл по частям:

 .
.
Поскольку функция  стремится к
стремится к 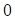 быстрее, чем возрастает
быстрее, чем возрастает  , то при подстановке верхнего предела интегрирования первое слагаемое обращается в
, то при подстановке верхнего предела интегрирования первое слагаемое обращается в 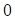 , а при подстановке нижнего предела принимает значение
, а при подстановке нижнего предела принимает значение 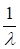 . В результате имеем:
. В результате имеем:
 .
.
Так как средняя наработка до отказа элемента  , то
, то
 .
.
Таким образом, при ненагруженном резервировании средняя наработка до отказа системы в 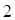 раза превышает среднюю наработку до отказа элемента, тогда как при нагруженном резервировании это соотношение составляет
раза превышает среднюю наработку до отказа элемента, тогда как при нагруженном резервировании это соотношение составляет  , то есть ненагруженное резервирование обеспечивает более высокие показатели надежности, чем нагруженное.
, то есть ненагруженное резервирование обеспечивает более высокие показатели надежности, чем нагруженное.
Однако при использовании ненагруженного резервирования возможен перерыв в работе системы на время выключения отказавшего основного и включения резервного элемента. Поэтому в тех случаях, когда по каким-либо причинам, например, по условиям обеспечения безопасности, перерыв в работе системы недопустим, применяют нагруженное резервирование.
На электровозах по схеме нагруженного резервирования работают мотор-компрессоры, а по схеме ненагруженного резервирования – токоприемники. Отказ основного токоприемника обнаруживается сразу по отсутствию тягового усилия и не приводит к опасной ситуации. Если бы мотор-комрессоры были включены по схеме ненагруженного резервирования, то отказ основного мотор-компрессора мог быть не обнаружен сразу, что могло бы привести к истощению тормозной магистрали из-за утечек сжатого воздуха, что приводит к нарушению безопасности движения.
Пример 3.2. Резервирование с восстановлением работоспособности отказавших элементов.
Рассмотрим функционирование системы, состоящей из 2-х одинаковых элементов, работающих в режиме нагруженного резервирования. После отказа одного из элементов немедленно начинается восстановление его работоспособности. Если отказавший элемент восстанавливается прежде, чем откажет 2-ой элемент, то система возвращается в исходное состояние. Если в течение времени восстановления отказавшего элемента происходит отказ и второго элемента, то система полностью отказывает, прекращается ее функционирование, но при этом продолжается восстановление работоспособности элемента, отказавшего первым. После его восстановления система вступает в работу, и одновременно начинается восстановление второго элемента, после его восстановления система возвращается в исходное состояние. Далее процесс функционирования происходит аналогично.
Допустим, что время безотказной работы обоих элементов и время восстановления их работоспособности являются случайными величинами, распределенными по экспоненциальному закону.
Обозначим
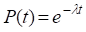 – вероятность безотказной работы одного элемента;
– вероятность безотказной работы одного элемента;
 – среднее время безотказной работы (средняя наработка до отказа);
– среднее время безотказной работы (средняя наработка до отказа);
 – вероятность восстановления работоспособности отказавшего элемента;
– вероятность восстановления работоспособности отказавшего элемента;
 – интенсивность восстановления;
– интенсивность восстановления;
 – среднее время восстановления;
– среднее время восстановления;
 – вероятность отказа одного элемента за бесконечно малый промежуток времени
– вероятность отказа одного элемента за бесконечно малый промежуток времени  ;
;
 – вероятность безотказной работы элемента за время
– вероятность безотказной работы элемента за время  ;
;
 – вероятность восстановления работоспособности одного элемента за время
– вероятность восстановления работоспособности одного элемента за время  ;
;
 – вероятность того, что за время
– вероятность того, что за время  работоспособность отказавшего элемента не будет восстановлена.
работоспособность отказавшего элемента не будет восстановлена.
При сделанных допущениях об экспоненциальном характере распределений времени безотказной работы и времени восстановления процесс функционирования рассматриваемой системы является марковским [2].
В процессе функционирования рассматриваемая система может находиться в следующих состояниях:
1. Оба элемента работают;
2. Один элемент работает, второй отказал и восстанавливается;
3. Оба элемента отказали, один из них восстанавливается, система отказала.
Если система находится в 1-ом состоянии, то за время  она перейдет во 2-ое состояние, при отказе одного из элементов. Если ни один из элементов не отказал, то система остается в 1-ом состоянии.
она перейдет во 2-ое состояние, при отказе одного из элементов. Если ни один из элементов не отказал, то система остается в 1-ом состоянии.
Вероятность безотказной работы двух элементов равна
 .
.
Пренебрегая бесконечно малой высшего порядка  , получаем, что вероятность
, получаем, что вероятность 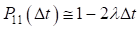 .
.
Вероятность отказа одного из двух элементов, то есть 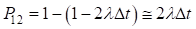 .
.
Если система находится во 2-ом состоянии, то:
– Она перейдет в 1-ое состояние, если за время  произойдет восстановление отказавшего элемента и не откажет второй элемент
произойдет восстановление отказавшего элемента и не откажет второй элемент  .
.
– Она перейдет в 3-е состояние, если за время  не будет восстановлен отказавший элемент, и откажет второй элемент
не будет восстановлен отказавший элемент, и откажет второй элемент  .
.
– Она останется во 2-ом состоянии, если не перейдет ни в 1-ое, ни в 3-е состояние  .
.
Если система находится в 3-ем состоянии, то она перейдет во 2-ое, если за время  закончится восстановление работоспособности элемента, отказавшего первым
закончится восстановление работоспособности элемента, отказавшего первым  .
.
Если восстановление работоспособности отказавшего элемента за время  не закончится, то система останется в 3-ем состоянии
не закончится, то система останется в 3-ем состоянии 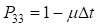 .
.
Граф переходов рассматриваемой системы изображен на рис. 3.3.

Рис. 3.3. Граф переходов системы с резервированием и восстановлением работоспособности отказавших элементов
Уравнения Колмогорова, связывающие между собой вероятности состояний системы в моменты  и
и  , записываются в виде:
, записываются в виде:

После соответствующих преобразований эта система конечно-разностных уравнений превращается в систему дифференциальных уравнений

Граф переходов, показанный на рис. 3.3, является связным, поэтому процесс функционирования рассматриваемой системы имеет установившийся режим, в котором вероятности всех состояний перестают зависеть от времени, принимают финальные значения, а их производные равны нулю, при этом дифференциальные уравнения превращаются в алгебраические.

Полученную систему алгебраических уравнений решаем при условии
 (3.2)
(3.2)
Из первого уравнения находим
 .
.
Из третьего уравнения выражаем
 .
.
Полученные выражения  и
и  подставляем в (3.2).
подставляем в (3.2).
 .
.
Отсюда
 .
.
Рассматриваемая система находится в работоспособном состоянии и выполняет свои функции, пребывая в состояниях 1 или 2, поэтому коэффициент готовности этой системы 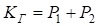 , то есть
, то есть
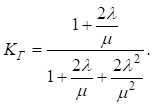 (3.3)
(3.3)
Рассчитаем значение  при
при  и
и 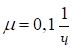 , то есть каждый элемент отказывает в среднем один раз за сто часов работы, а среднее время восстановления составляет 10 часов.
, то есть каждый элемент отказывает в среднем один раз за сто часов работы, а среднее время восстановления составляет 10 часов.
Расчет коэффициента готовности для нерезервированной системы дает значение
 .
.
Расчет по формуле (3.3) дает значение
 .
.
Таким образом, введение резервирования существенно повышает надежность системы, приблизив вероятность ее нахождения в работоспособном состоянии практически к единице, то есть резервирование элементов с восстановлением работоспособности после отказа является эффективным способом повышения надежности ТО.
Пример 3.3. Определить вероятность безотказной работы системы, изображенной на рис. 3.4, если элементы  и
и  отказывают с интенсивностью
отказывают с интенсивностью  , а элементы
, а элементы  и
и  с интенсивностью
с интенсивностью 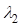 .
.

Рис. 3.4. Структурная схема
Равнонадежные элементы  и
и  соединены параллельно. Вероятность отказа подсистемы
соединены параллельно. Вероятность отказа подсистемы  определяется
определяется
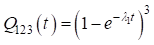 .
.
Вероятность безотказной работы  равна
равна

Равнонадежные элементы  и
и  также соединены параллельно. Вероятность безотказной работы подсистемы
также соединены параллельно. Вероятность безотказной работы подсистемы  определяется по формуле
определяется по формуле
 .
.
Подсистемы  и
и  соединены последовательно, поэтому вероятность безотказной работы системы
соединены последовательно, поэтому вероятность безотказной работы системы
 .
.

Пример 3.4. Определить вероятность безотказной работы системы, изображенной на рис. 3.5. Все элементы этой системы равнонадежны, интенсивность их отказов равна  .
.

Рис. 3.5. Структурная схема
Элементы  и
и  соединены по схеме ненагруженного резервирования. Вероятность безотказной работы подсистемы
соединены по схеме ненагруженного резервирования. Вероятность безотказной работы подсистемы  определяется по формуле.
определяется по формуле.
 .
.
Элементы  и
и  соединены по схеме нагруженного резервирования. Вероятность безотказной работы подсистемы
соединены по схеме нагруженного резервирования. Вероятность безотказной работы подсистемы  определяется по формуле
определяется по формуле
 .
.
Подсистемы  и
и  соединены последовательно, поэтому вероятность безотказной работы системы
соединены последовательно, поэтому вероятность безотказной работы системы

 .
.
 .
.
Пример 3.5. Определить вероятность безотказной работы восьмиосного электровоза, работающего со 100%-ным использованием силы тяги. Вероятность безотказной работы одного тягового двигателя равна 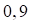 .
.
Отказ электровоза при 100%-ном использовании силы тяги наступает при отказе одного из восьми тяговых двигателей, то есть в рассматриваемой ситуации все двигатели соединены последовательно с точки зрения надежности. Вероятность безотказной работы электровоза определяется по формуле
 ,
,
то есть вероятность безотказной работы электровоза примерно в  раза ниже вероятности безотказной работы одного тягового двигателя.
раза ниже вероятности безотказной работы одного тягового двигателя.
Пример 3.6. Восьмиосный электровоз работает с недоиспользованием силы тяги, и его отказ наступает после отказа четырех тяговых двигателей (то есть система тяговых двигателей имеет так называемую функциональную избыточность). Рассчитать вероятность отказа электровоза, если наработка на отказ каждого тягового двигателя распределена по экспоненциальному закону с интенсивностью  .
.
Решение этой задачи осуществляется на основе методов теории марковских процессов.
Состояние электровоза будем различать по числу отказавших тяговых двигателей. Состояния:
0 – все двигатели работают;
1 – отказал первый тяговый двигатель;
2 – отказали два тяговых двигателя;
3 – отказали три тяговых двигателя;
4 – отказали четыре тяговых двигателя.
Вероятность отказа одного тягового двигателя за время  равна
равна  , а вероятность безотказной работы
, а вероятность безотказной работы  .
.
Вероятность безотказной работы  тяговых двигателей за время
тяговых двигателей за время  составляет
составляет  .
.
Вероятность отказа одного из  тяговых двигателей за время
тяговых двигателей за время  равна
равна 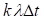 .
.
Граф переходов электровоза из одного состояния в другое показан на рис. 3.6.

Рис. 3.6. Граф переходов электровоза
Уравнения Колмогорова рассматриваемой системы имеют следующий вид:

После соответствующих преобразований система конечно-разностных уравнений превращается в систему дифференциальных уравнений:

Численное решение системы дифференциальных уравнений при начальных условиях  и значении
и значении  осуществлялось на ЭВМ в вычислительной среде Mathcad.
осуществлялось на ЭВМ в вычислительной среде Mathcad.
Результаты решения в виде зависимостей вероятностей состояний от времени представлены на рис. 3.7. Из этого графика видно, что, например, при наработке  вероятность отказа электровоза составляет примерно
вероятность отказа электровоза составляет примерно  . При наработке
. При наработке  электровоз отказывает с вероятностью равной
электровоз отказывает с вероятностью равной  .
.

Рис. 3.7. Зависимости вероятностей состояния электровоза от времени
Пример 3.7. Интенсивность отказов тягового двигателя возрастает на 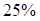 от начального уровня после отказа очередного двигателя. Рассчитать вероятность отказа восьмиосного электровоза, если он наступает после отказа 4-х тяговых двигателей. Наработка на отказ каждого тягового двигателя распределена по экспоненциальному закону с начальным уровнем интенсивности отказов
от начального уровня после отказа очередного двигателя. Рассчитать вероятность отказа восьмиосного электровоза, если он наступает после отказа 4-х тяговых двигателей. Наработка на отказ каждого тягового двигателя распределена по экспоненциальному закону с начальным уровнем интенсивности отказов  .
.
Эта задача решается аналогично предыдущей. Состояния электровоза те же.
Интенсивность отказов тягового двигателя в 0-ом состоянии равна  , в 1-ом –
, в 1-ом –  , во 2-ом –
, во 2-ом –  и в 3-ем –
и в 3-ем –  .
.
Граф переходов электровоза из одного состояния в другое показан на рис. 3.8.

Рис. 3.8. Граф переходов электровоза
Уравнения Колмогорова записываются в следующем виде:
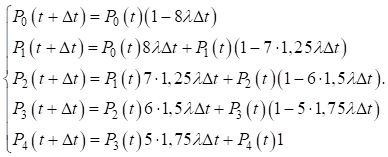
Выполнив необходимые преобразования, получим систему дифференциальных уравнений при значении 

Численное решение данной системы дифференциальных уравнений при начальных условиях  так же производилось на ЭВМ в вычислительной среде Mathcad.
так же производилось на ЭВМ в вычислительной среде Mathcad.
Результаты решения представлены на рис. 3.9, из которого видно, что при наработке  вероятность отказа электровоза превышает
вероятность отказа электровоза превышает  , то есть возросла более чем в
, то есть возросла более чем в  раза по сравнению с ранее рассмотренным случаем. Электровоз отказывает с вероятностью
раза по сравнению с ранее рассмотренным случаем. Электровоз отказывает с вероятностью  при наработке около 1500 ч.
при наработке около 1500 ч.

Рис. 3.9. Зависимости вероятностей состояния электровоза от времени
Таким образом, возрастание интенсивности отказов тяговых двигателей, которое происходит вследствие увеличения нагрузок оставшихся двигателей после отказа некоторых из них, приводит к существенному снижению надежности электровоза.
Пример 3.8. Устройство имеет отказы трёх видов, каждое из которых возникает со своей интенсивностью  , а восстановление после отказа каждого вида производится со своей интенсивностью
, а восстановление после отказа каждого вида производится со своей интенсивностью  . Определить вероятность безотказной работы устройства при продолжительной его эксплуатации.
. Определить вероятность безотказной работы устройства при продолжительной его эксплуатации.
Три возможных состояния устройства: 0 – исправно и работает; 1 – восстанавливается после отказа первого вида; 2 – восстанавливается после отказа второго вида; 3 – восстанавливается после отказа третьего вида.

Рис. 3.10. Граф переходов
Вероятность перехода устройства из  -го в
-го в  -е состояние (
-е состояние ( ) за промежуток времени
) за промежуток времени  равна вероятности отказа соответствующего вида
равна вероятности отказа соответствующего вида  , где
, где  . Вероятность перехода устройства из
. Вероятность перехода устройства из  -го (
-го ( ) в
) в  -е состояние за промежуток времени
-е состояние за промежуток времени  равна вероятностям восстановления работоспособного состояния после отказа
равна вероятностям восстановления работоспособного состояния после отказа  -го вида
-го вида  , где
, где  .
.
Уравнения Колмогорова записываются в следующем виде:

После всех необходимых преобразований получаем систему дифференциальных уравнений

В установившемся режиме, который имеет процесс функционирования рассматриваемого устройства, так как граф его переходов является связным, система дифференциальных уравнений превращается в систему алгебраических уравнений

Из полученных уравнений выражаем вероятности  и
и  через вероятность
через вероятность  .
.
Из второго уравнения выражаем
 .
.
Из третьего уравнения выражаем
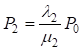 .
.
Из четвертого уравнения выражаем
 .
.
Подставив эти вероятности в уравнение  , получим
, получим
 .
.
Отсюда
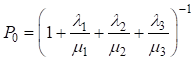 .
.
Рассматриваемое устройство работоспособно, только находясь в  -м состоянии, поэтому вероятность работоспособного состояния при длительной эксплуатации, то есть коэффициент готовности, равна
-м состоянии, поэтому вероятность работоспособного состояния при длительной эксплуатации, то есть коэффициент готовности, равна  .
.
Обобщая полученный результат, можно видеть, что если устройство имеет отказы  видов и все
видов и все  ,
,  ,
, 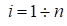 , то
, то
 .
.
Показатели безотказности  и ремонтопригодности
и ремонтопригодности  определяются по статистическим данным в процессе эксплуатации рассматриваемого устройства.
определяются по статистическим данным в процессе эксплуатации рассматриваемого устройства.
4. Определение показателей безотказности оборудования подвижного состава по информации о контролируемых параметрах
Для каждого технического изделия имеется большое число признаков (параметров), как правило, изменяющихся в процессе его эксплуатации, по значениям которых делается вывод о техническом состоянии рассматриваемого оборудования. Таким образом, в эксплуатации периодически (или постоянно) оценивают техническое состояние оборудования – отдельных узлов и агрегатов подвижного состава. В ходе оценки технического состояния получают конкретные значения диагностических признаков или контролируемых параметров, которые затем сравниваются с установленными требованиями и нормами.
При диагностировании путем оценки контролируемого параметра информация о техническом состоянии оборудования получается в виде числовых значений контролируемых параметров, характеризующих это состояние. Такой вид диагностирования используется в основном для узлов и деталей ТПС, подверженных износу и старению. В этом случае в качестве контролируемых параметров выступают геометрические размеры узлов и деталей, уровень звукового давления, издаваемый в процессе работы, температура нагрева и др.
Если измерение значений контролируемого параметра и наработки соответствующего узла вести от момента полного его восстановления (от номинальной величины), то ряд его значений, полученный при нескольких последовательных измерениях, будет представлять реализацию контролируемого параметра. Эти реализации удобно представить в виде диаграмм рассеивания. Различают два вида контролируемых параметров: увеличивающиеся и уменьшающиеся (рис. 4.1).
| а) | б) |
 |  |
Рис. 4.1. Примеры реализаций контролируемых параметров: а) увеличивающегося; б) уменьшающегося.
По мере изменения контролируемого параметра в какой-то момент времени происходит выход его за установленное предельное (допустимое) значение  , то есть наступает отказ соответствующего оборудования.
, то есть наступает отказ соответствующего оборудования.
В большинстве случаев в процессе эксплуатации ТПС значения контролируемых параметров не выходят за предел  , так как его величина определяется необходимостью проведения очередного планово-предупредительного ремонта соответствующего оборудования. То есть наработка оборудования на момент проведения планово-предупредительного ремонта не является наработкой до отказа. Таким образом, использовать рассмотренные ранее способы определения показателей безотказности не представляется возможным.
, так как его величина определяется необходимостью проведения очередного планово-предупредительного ремонта соответствующего оборудования. То есть наработка оборудования на момент проведения планово-предупредительного ремонта не является наработкой до отказа. Таким образом, использовать рассмотренные ранее способы определения показателей безотказности не представляется возможным.
Контролируемый параметр изнашиваемой детали при фиксированной наработке является непрерывной случайной величиной, закон распределения которой может быть представлен плотностью распределения. Вид предполагаемого закона распределения выбирается, исходя из анализа физических процессов, протекающих при изнашивании или старании узлов и агрегатов, работоспособность которых оценивается соответствующим контролируемым параметром.
Теоретически и многочисленными опытами установлено, что случайная величина – контролируемый параметр, характеризующая изнашивание оборудования ТПС, при фиксированном значении наработки хорошо описывается нормальным законом распределения, что является следствием действия закона больших чисел. Согласно этому закону, если случайная величина подвержена действию большого числа случайных факторов, среди которых нельзя выявить преобладающего, то есть каждый из них оказывает на нее приблизительно одинаковое влияние, распределение ее подчиняется нормальному закону.
На процесс изнашивания оборудования ТПС воздействует большое число случайных факторов: химический состав материала, качество изготовления, прочностные характеристики, климатические и метеорологические условия эксплуатации, нагрузочные режимы и частоты их повторяемости (количество пусков и остановок, режимы тяги и торможения, продолжительность движения с максимальной нагрузкой и т.п.), температурные условия эксплуатации, степень влажности атмосферы и ее запыленность, насыщенность поверхностей трения абразивными частицами, зависящая от интенсивности подачи песка, состояние пути и зависящие от него динамические нагрузки на оборудование ТПС, а также многие другие факторы.
Среди перечисленных факторов невозможно выделить преобладающий, каждый из них оказывает приблизительно одинаковое влияние на процесс изнашивания деталей ТПС, поэтому их контролируемые параметры при фиксированной наработке распределяются по нормальному закону.
Чтобы прогнозировать процесс изменения контролируемых параметров рассматриваемых деталей и узлов с целью определения их показателей безотказности и долговечности необходимо определить вид и параметры аналитических зависимостей  числовых характеристик закона распределения от наработки: средних значений
числовых характеристик закона распределения от наработки: средних значений 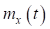 и среднеквадратических отклонений
и среднеквадратических отклонений  .
.
В общем виде эту зависимость можно представить в виде некоторой нелинейной функции  одного аргумента
одного аргумента  , в выражение которой входит
, в выражение которой входит 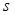 параметров
параметров  . С помощью этой функции необходимо аппроксимировать эмпирическое поле корреляции, заданное в виде
. С помощью этой функции необходимо аппроксимировать эмпирическое поле корреляции, заданное в виде  точек
точек  при
при 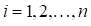 , где под
, где под  понимается один из параметров рассматриваемого закона распределения.
понимается один из параметров рассматриваемого закона распределения.
Экстраполяцию процессов изменения контролируемых параметров оборудования ТПС, имеющих нормальный закон распределения, целесообразно осуществлять в область больших наработок на основе числовых характеристик:  – среднего значения и
– среднего значения и  – среднеквадратического отклонения, рассчитанных при фиксированных значениях наработки
– среднеквадратического отклонения, рассчитанных при фиксированных значениях наработки  .
.
Параметры функции  находятся методом «наименьших квадратов», условие которого записывается в виде:
находятся методом «наименьших квадратов», условие которого записывается в виде:
 (4.1)
(4.1)
Зависимости 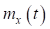 и
и  изнашиваемых деталей ТПС, как правило, хорошо описывается линейными функциями. Теоретически и практически доказано, что обычно реализация износа деталей локомотивов имеет вид, представленный на рис. 4.2.
изнашиваемых деталей ТПС, как правило, хорошо описывается линейными функциями. Теоретически и практически доказано, что обычно реализация износа деталей локомотивов имеет вид, представленный на рис. 4.2.

Рис. 4.2. Реализация контролируемого параметра
Участок I этой зависимости характеризует приработочный период, в котором деталь изнашивается с повышенной интенсивностью. Это объясняется притиранием сопряженных поверхностей, в результате которого происходит выравнивание свойств этих поверхностей, процесс изнашивания стабилизируется и наступает период нормальной эксплуатации (участок II), в течение которого интенсивность износа постоянна и имеет наименьшее из всех возможных значений.
Период нормальной эксплуатации заканчивается и наступает период усиленного износа (участок III), когда интенсивность износа детали снова увеличивается в результате возникновения и роста паразитных перемещений деталей, например, проскальзывания колес по рельсам, ударов и перекосов в шарнирах и т.д.
На практике измерения контролируемых параметров оборудования ТПС производят обычно не чаще, чем на текущем ремонте ТР-1, а приработка до первого ТР-1 успевает закончиться, поэтому статистические данные о значениях контролируемых параметров не содержат обычно информации о протекании процесса изнашивания в периоде приработки.
Кроме того, допуски на значения контролируемых параметров устанавливаются так, чтобы предупредить наступление периода усиленного износа, поэтому наблюдение за износом заканчивается прежде, чем наступает этот период.
Вследствие указанных причин полученные на практике значения контролируемых параметров представляют только участок нормальной эксплуатации (участок II), в котором зависимости этих параметров от наработки близки к линейным. Поэтому эмпирические зависимости числовых характеристик  и
и  изнашиваемого оборудования достаточно хорошо аппроксимируются линейной функцией вида
изнашиваемого оборудования достаточно хорошо аппроксимируются линейной функцией вида
 (4.2)
(4.2)
Условие метода «наименьших квадратов» в этом случае запишется
 (4.3)
(4.3)
В выражении (4.3)  соответствует аппроксимации зависимости
соответствует аппроксимации зависимости 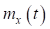 , а
, а  – зависимости
– зависимости  .
.
Коэффициент  зависимости
зависимости  по методу «наименьших квадратов» определяется как:
по методу «наименьших квадратов» определяется как:
 (4.4)
(4.4)
где  – коэффициент корреляции между случайными величинами и
– коэффициент корреляции между случайными величинами и  ;
;
 ,
,  – среднеквадратические отклонения, соответственно для
– среднеквадратические отклонения, соответственно для  и
и  .
.
 (4.5)
(4.5)
 (4.6)
(4.6)
где  – среднее значение величины
– среднее значение величины 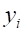 ;
;
 – среднее значение наработки.
– среднее значение наработки.
Коэффициент  уравнения регрессии определяется как:
уравнения регрессии определяется как:
 (4.7)
(4.7)
Коэффициент корреляции  характеризует тесноту линейной связи между случайными величинами
характеризует тесноту линейной связи между случайными величинами  и
и  и определяется как:
и определяется как:
 (4.8)
(4.8)
где 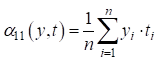 – второй смешанный начальный момент случайных величин
– второй смешанный начальный момент случайных величин  и
и  .
.

Рис. 4.3. Зависимости от наработки среднего значения и среднеквадратического отклонения толщины бандажа
Физический смысл коэффициентов  и
и  уравнения регрессии среднего значения следующий:
уравнения регрессии среднего значения следующий:
–коэффициент  есть тангенс угла наклона регрессии, соответственно он характеризует интенсивность изнашивания, мм/тыс. км.;
есть тангенс угла наклона регрессии, соответственно он характеризует интенсивность изнашивания, мм/тыс. км.;
–коэффициент  характеризует среднее номинальное значение контролируемого параметра, т. е. его величину в момент начала эксплуатации, мм.
характеризует среднее номинальное значение контролируемого параметра, т. е. его величину в момент начала эксплуатации, мм.
На основании рассчитанных и построенных зависимостей 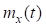 и
и  становится возможным проанализировать и спрогнозировать процесс изнашивания для расчета показателей безотказности оборудования.
становится возможным проанализировать и спрогнозировать процесс изнашивания для расчета показателей безотказности оборудования.
Для прогнозирования процесса изнашивания зависимости 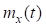 и
и  экстраполируются в область больших наработок, т. е. предполагается, что изнашивание детали происходит в пределах периода нормальной эксплуатации. Это обеспечивается правильным выбором допуска на величину износа рассматриваемой детали.
экстраполируются в область больших наработок, т. е. предполагается, что изнашивание детали происходит в пределах периода нормальной эксплуатации. Это обеспечивается правильным выбором допуска на величину износа рассматриваемой детали.
Далее, подставляя значение пробега  в выражения уравнений регрессий, рассчитывают числовые характеристики
в выражения уравнений регрессий, рассчитывают числовые характеристики 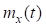 и
и  распределения контролируемых параметров в области экстраполяции и строят кривые плотности распределения (рис. 4.4).
распределения контролируемых параметров в области экстраполяции и строят кривые плотности распределения (рис. 4.4).

Рис. 4.4. Определение вероятности отказа (на примере толщины бандажей колесных пар)
Как видно из рис. 4.4, с ростом наработки (пробега)  увеличивается вероятность того, что значение контролируемого параметра выйдет за пределы установленного допуска (заштрихованная часть площади, ограниченной кривой плотности распределения параметра).
увеличивается вероятность того, что значение контролируемого параметра выйдет за пределы установленного допуска (заштрихованная часть площади, ограниченной кривой плотности распределения параметра).
Выход контролируемого параметра за установленный допуск  классифицируется как отказ детали, износ которой он характеризует.
классифицируется как отказ детали, износ которой он характеризует.
Таким образом, с увеличением пробега  возрастает вероятность отказа детали
возрастает вероятность отказа детали 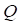 и, соответственно, уменьшается вероятность безотказной работы детали
и, соответственно, уменьшается вероятность безотказной работы детали  .
.
Для увеличивающегося контролируемого параметра (например, проката бандажа по кругу катания), при нормальном законе распределения вероятность отказа при заданном пробеге  рассчитывается по формуле
рассчитывается по формуле
 (4.9)
(4.9)
| |
Если значение контролируемого параметра уменьшается с увеличением пробега (например, толщина бандажа), то вероятность отказа определяется
 (4.10)
(4.10)
Интеграл, входящий в выражения (4.9) и (4.10), не выражается в элементарных функциях, поэтому его значение находится численными методами.
Функция вероятности безотказной работы определяется как
 (4.11)
(4.11)
На основании полученных функциональных зависимостей  и
и  можно рассчитать показатели безотказности и долговечности
можно рассчитать показатели безотказности и долговечности  ,
,  ,
, 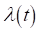 и
и  .
.
Пример 4.1. Расчет функции распределения ресурса и определение гамма-процентного ресурса по информации о толщине зуба шестерни тягового редуктора.
Исходные данные для расчёта приведены в таблице 4.1.
Таблица 4.1
|
| 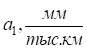 | -0,0017 |
 | 15,5 | |
|
|  | 0,0003 |
 | 0,3 | |
| Допуск |  | 12,3 |
Решение.
1) Построение зависимостей среднего значения 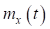 и среднеквадратического отклонения
и среднеквадратического отклонения  контролируемого параметра от наработки:
контролируемого параметра от наработки:


Тогда


Определение интервала наработки  для расчета:
для расчета:


Тогда

 тыс.км.
тыс.км.

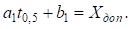
Тогда

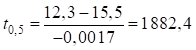 тыс.км.
тыс.км.
 тыс.км.
тыс.км.
Здесь: 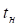 – начальное значение наработки, тыс.км;
– начальное значение наработки, тыс.км;
 – наработка, соответствующая вероятности отказа равной 0,5, тыс.км;
– наработка, соответствующая вероятности отказа равной 0,5, тыс.км;
 – интервал наработки для расчета значений функции распределения ресурса
– интервал наработки для расчета значений функции распределения ресурса  , тыс.км.
, тыс.км.
С учетом вышеизложенного и для дальнейшего удобства построения примем  тыс.км с принятыми интервалами наработки
тыс.км с принятыми интервалами наработки  , а также
, а также 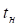 и
и  .
.
Построим графики зависимостей среднего значения 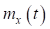 и среднеквадратического отклонения
и среднеквадратического отклонения  контролируемого параметра от наработки.
контролируемого параметра от наработки.
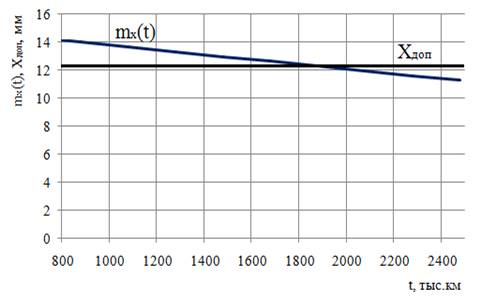
Рис. 4.5. Зависимость среднего значения  толщины зуба шестерни от наработки
толщины зуба шестерни от наработки

Рис. 4.6. Зависимость среднеквадратического отклонения 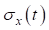 толщины зуба шестерни от наработки
толщины зуба шестерни от наработки
2) Расчет вероятности отказа и функции распределения  . Полученные данные сведены в таблице 4.2.
. Полученные данные сведены в таблице 4.2.
Таблица 4.2
 , тыс. км , тыс. км | 884,6 | 1084,2 | 1283,7 | 1483,3 | 1682,8 | 1882,4 | 2082 | 2281,5 | 2482 |
 | 14 | 13,66 | 13,32 | 12,98 | 12,64 | 12,30 | 11,96 | 11,62 | 11,28 |
 | 0,57 | 0,63 | 0,69 | 0,74 | 0,80 | 0,86 | 0,92 | 0,98 | 1,04 |
 | -3 | -2,17 | -1,49 | -0,91 | -0,42 | 0 | 0,37 | 0,69 | 0,97 |
| Q(t)=F(t) | 0,00135 | 0,015003 | 0,068112 | 0,181411 | 0,337243 | 0,5 | 0,644309 | 0,754903 | 0,833977 |
 | 0,99865 | 0,984997 | 0,931888 | 0,818589 | 0,662757 | 0,5 | 0,355691 | 0,245097 | 0,166023 |
Где  – нормированное и центрированное значение контролируемого параметра:
– нормированное и центрированное значение контролируемого параметра:

Значения функции распределения и вероятности отказа Q(t)=F(t)=Ф(z) определяются по функции Лапласа в зависимости от значения нормированного и центрированного контролируемого параметра  . Соответственно,
. Соответственно, 
По результатам расчетов построена функция распределения ресурса зуба шестерни  и функция вероятности безотказной работы P(t).
и функция вероятности безотказной работы P(t).

Рис. 4.7. Функции распределения ресурса зуба шестерни  и вероятности безотказной работы Р(t)
и вероятности безотказной работы Р(t)
3) Расчет и построение функции плотности распределения параметра  для двух значений наработок
для двух значений наработок 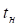 и
и  .
.
Вероятность отказа для уменьшающегося параметра найдем по формуле:

Для нормального закона распределения:
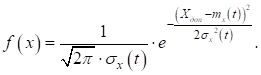
В нашем случае:

Тогда
при  тыс.км:
тыс.км:
 мм;
мм;
 мм;
мм;
 мм;
мм;
 мм.
мм.
при t =1882,4 тыс.км:
 мм;
мм;
 мм;
мм;
 2020-06-08
2020-06-08 1593
1593
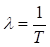 –
–