Интегральная теорема Муавра – Лапласа

При большом числе испытаний 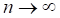 вероятности наступления события А в каждом испытании р, отличной от 0 и 1, и при выполнении условия 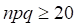, вероятность  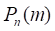того, что в n независимых испытаниях событие А наступит от а до b раз, определяется соответствии с интегральной теоремой Муавра — Лапласа:

               (1.26)

где n – число испытаний Бернулли;

m – число испытаний, в которых наступило событие А;

р=Р(А) – вероятность наступления события А в каждом испытании;

q=1-р – вероятность противоположного события ();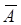

 – функция Лапласа (табл. 1 Приложений).

Функция Лапласа Ф(t) представляет собой функцию стандартного нормального закона распределения и будет рассмотрена более подробно теме «Нормальный закон распределения» (гл. 7).

Здесь отметим только ее основные свойства, необходимые для применения рассматриваемой теоремы.

Функция Лапласа:

1. Ф(t) — нечетная функция, т. е. Ф(-t)=-Ф(t)/

2. Ф(t) — монотонно возрастающая функция, т. е. Ф(t)→1 при t→+ ; при t>5 можно считать Ф(t) 1.

 

Задачи, приводящие к интегральной теореме Муавра – Лапласа.

Пусть производится n независимых испытаний, в каждом из которых вероятность наступления события А равна р:

а) вероятность того, что частота наступления (частость) события А отклонится от вероятности p (по модулю) не более, чем на величину :

;                                             (1.27)

б) наименьшее число испытаний, которое нужно провести, чтобы с вероятностью, равной р, можно было гарантировать, что частота наступления события А отклонится от вероятности/? не более, чем на :

;                       (1.28)

в) при данной вероятности  и числе испытаний n границы возможных изменений отклонения частоты наступления события А от вероятности р:

;                         (1.29)

г) вероятность того, что m наступлений события А отличается от произведения nр (по модулю) не более, чем на величину :

                                                                  (1.30)

или в других обозначениях: .

 

§ 4.4. Теоремы Пуассона [3]

При большом числе испытаний 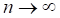, постоянной малой вероятности наступления события А в каждом испытании , и при выполнении условия , вероятность 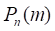 того, что в n независимых испытаниях событие А наступит ровно m раз, определяется соответствии с теоремой Пуассона:

                                                (1.31)

где n — число испытаний Бернулли;

m — число испытаний, в которых наступило событие А;

 — параметр Пуассоновского распределения, называемый еще средней интенсивностью.

Теорему можно доказать путем замены в формуле Бернулли вероятности р на  вычисления ее предела при /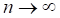

Значения функции Пуассона 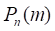 также могут быть определены по табл. 8 Приложения для заданных значений m и .

Случайные события, к которым может быть применена теорема Пуассона, называют еще редкими событиями ввиду малой вероятности наступления события А в каждом испытании.

[1] Бернулли (Bernoulli) Якоб (1654-1705) – швейцарский ученый-математик, профессор математики Базельского университета, родоначальник знаменитой семьи ученых.

[2] Муавр (Moivre) Абрахам де (1667-1754) – английский математик. Лаплас (Laplace) Пьер Симон (1749-1827) – французский астроном, математик и физик. Теорема доказана П. Лапласом в книге «Аналитическая теория вероятностей» (1812). Один частный случай был известен ПА. Муавру (1730), в связи с чем и называется теоремой Муавра – Лапласа.

[3] Пуассон (Poisson) Симеон Дени (1781-1840), французский ученый, выдающийся математик и физик, профессор Парижского университета.