Обратный обратимый цикл Карно

Цикл состоит из следующих процессов (рис.4.6):

 

12 – адиабатное расширение (dq=0);

23 – изотермическое расширение (Т₂=const) с подводом q₂ от «холодного» источника;

34 – адиабатное сжатие (dq=0);

41 – изотермическое сжатие (Т₁=const) с отводом q₁ в «горячий» источник.

Рис. 4.6.

Для осуществления цикла затрачивается работа .

Холодильный коэффициент                     (4.6)

 увеличивается при уменьшении T₁ и увеличении T₂.

Отопительный коэффициент                    (4.7)

 увеличивается при уменьшении T₁ и увеличении T₂.

Приведенная теплота

В прямом обратимом цикле Карно

.

Алгебраическая сумма 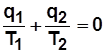; ,                   (4.8)

где  - приведенная теплота.

· В обратимом цикле Карно алгебраическая сумма приведенных теплот равна нулю.

В необратимом цикле Карно, протекающем с конечной скоростью, и конечной разностью Т и Т_р.т. тепловых источников и рабочего тела, при расширении Т₁>Т_1р.т., при сжатии Т₂<Т_2р.т.. Поэтому

.

Алгебраическая сумма .                    (4.9)

· В необратимом цикле Карно алгебраическая сумма приведенных теплот меньше нуля.

Произвольные обратимый и необратимый циклы

Произвольный цикл заменяется суммой элементарных циклов Карно (рис. 4.7).

В обратимом цикле

Рис.7.7

+

В необратимом цикле

 (s-функция состояния),     (4.11)

В общем случае  (интеграл Клаузиуса); .

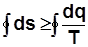Знак «=» относится к обратимому циклу, а знаки «<» и «>» - к необратимому.

Аналогично в процессах:

в обратимом ;  в необратимом .

При одинаковом изменении приведенной теплоты в необратимом процессе энтропия возрастает по сравнению с изменением S в обратимом процессе.

4.3. Энтропия необратимого процесса в замкнутой системе

В замкнутой системе (рис.7.8) при передаче теплоты от тела А с более высокой температурой телу Б энтропия тела А уменьшается, а тела Б возрастает: ;          ;

изменение энтропии системы

Рис. 4.8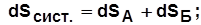                   

                     . (4.12)

    В необратимом процессе энтропия системы возрастает.