 Рассмотрим два цикла Карно (рис.4.9). В первом случае теплота dq подводится к рабочему телу непосред-ственно от тела А, во втором случае теплота dq вначале передается от тела А к телу Б, а затем – от тела Б рабочему телу.
Рассмотрим два цикла Карно (рис.4.9). В первом случае теплота dq подводится к рабочему телу непосред-ственно от тела А, во втором случае теплота dq вначале передается от тела А к телу Б, а затем – от тела Б рабочему телу.
Рис. 4.9
 ;
;  ;
;
разность работ этих циклов
 .
.
Изменение энтропии при передаче теплоты от тела А телу Б
 ;
;  ;
;
 . (4.13)
. (4.13)
С переходом теплоты на более низкий температурный уровень энтропия растет, а работоспособность рабочего тела снижается пропорционально росту энтропии.
Второй закон термодинамики: приведенная теплота; интеграл Клаузиуса; изменение приведенной теплоты и энтропии в обратимых и необратимых процессах и циклах; изменение энтропии как мера необратимости и потери работоспособности рабочего тела; формулировки второго закона термодинамики.
· Невозможно превратить в работу энергию какого-либо тела, не производя никакого другого действия, кроме охлаждения этого тела (Томсон, он же Кельвин).
· Перпетуум мобиле (вечный двигатель) второго рода невозможен (Оствальд). Перпетуум мобиле второго рода – воображаемый тепловой двигатель, в котором возможно стопроцентное превращение подведенной теплоты в работу.
· Теплота не может переходить от холодного к теплому телу сама собой, даровым процессом (Клаузиус).
Поршневые компрессоры
Поршневые компрессоры: работа одноступенчатого компрессора; параметры сжатия газа; затраты энергии на привод компрессора; многоступенчатое сжатие с промежуточным охлаждением газа; работа реального компрессора.
 Процессы, протекающие в поршневом компрессоре, представлены на рис. 5.1.
Процессы, протекающие в поршневом компрессоре, представлены на рис. 5.1.
На vp – диаграмме
а1 – процесс заполне-ния цилиндра рабочим телом
(p,T,r = сonst; M=var).
Рис. 5.1
Кривые 12,12’,12’’ – соответственно политропный, изотермический, адиабатный процессы сжатия (см. также диаграмму sT);
в реальных компрессорах n=1,2-1,25;
2б– вытеснение сжатого газа из цилиндра (p,T,r = const; M=var).
Работа на привод компрессора
 ;
;
 ~ пл. а12ба.
~ пл. а12ба.
Для 1 кг 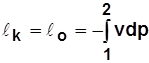 .
.
При изотермическом процессе сжатия
 , (5.1)
, (5.1)
где l - степень повышения давления, 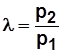 .
.
При политропном процессе сжатия
 . (5.2)
. (5.2)
 ; (5.3)
; (5.3)
Из sT – диаграммы
 ; (5.4)
; (5.4)
 ;
;
 . (5.5)
. (5.5)
При адиабатном процессе сжатия
 ; (5.6)
; (5.6)
 .
.
Многоступенчатый идеальный компрессор
Применяется при р2>0,8 МПа. Процессы в двухступенчатом компрессоре показаны на рис.5.2.
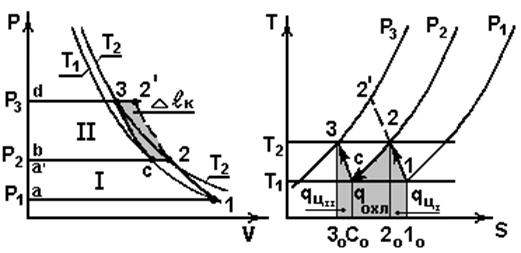
Рис. 5.2
Процессы
а1 – заполнение первой ступени рабочим телом;
12 – политропное сжатие в первой ступени;
2b – вытеснение сжатого газа из первой ступени;
bа ' (соответствует процессу 2с) – изобарное охлаждение газа
в охладителе до Т1;
а ' с – заполнение второй ступени;
с3 – политропное сжатие во второй ступени;
3d – вытеснение сжатого газа из второй ступени;
12 ' – политропное сжатие в одноступенчатом компрессоре.
В vP – координатах: В sT – координатах:
Пл. а12с3dа ~  . Пл. 10122010 ~
. Пл. 10122010 ~  .
.
Пл. а122’dа ~  при одноступенчатом Пл. 202сс020 ~
при одноступенчатом Пл. 202сс020 ~  .
.
сжатии.
Пл. c22’3c ~  - уменьшение
- уменьшение  . Пл. с0с330с0 ~
. Пл. с0с330с0 ~  .
.
При 2- ступенчатом сжатии Т3 < Т2’.
Обычно  и
и  ;
;  и
и  ,
,
где i – номер ступени; m – количество ступеней.
Для двухступенчатого компрессора  ;
;
при 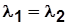 и
и  получим
получим  и
и  . (5.7)
. (5.7)
Для m – ступенчатого компрессора 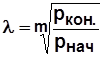 . (5.8)
. (5.8)
При одинаковой Т на входе в ступени  ,
,
где  - давление в начале сжатия в i - й ступени,
- давление в начале сжатия в i - й ступени,  .
.
Рабочий объем i - й ступени  . (5.9)
. (5.9)
Реальный компрессор
 В отличие от идеального реальный компрессор имеет вредный объем, давление при наполнении и нагнетании не остается постоянным. Цикл реального компрессора показан на рис. 5.3:
В отличие от идеального реальный компрессор имеет вредный объем, давление при наполнении и нагнетании не остается постоянным. Цикл реального компрессора показан на рис. 5.3:
НМТ – нижняя мертвая точка;
ВМТ – верхняя мертвая точка;
Vh – рабочий объем;
Vвр– вредный объем; 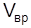 =(0,04-0,10)
=(0,04-0,10)  ;
;
а – относительный вредный объем;
 ; (5.10)
; (5.10)
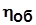 - объемный к.п.д;
- объемный к.п.д;
 . (5.11)
. (5.11)
Рис.5.3
В vp – координатах:
12 – политропное сжатие газа; n = 1,2…1,25 (при воздушном охлаждении до 1,35);
23 – вытеснение газа из цилиндра;
34 – расширение газа, оставшегося во вредном объеме;
41 – наполнение цилиндра новым зарядом.
При одинаковых показателях политропы n процессов сжатия и расширения  . С учетом этого после преобразования выражения (5.11) получим
. С учетом этого после преобразования выражения (5.11) получим  . (5.12)
. (5.12)
Цикловая подача газа, кг/цикл:
 . (5.13)
. (5.13)
Производительность компрессора:
· объемная, м3/ч:  , (5.14)
, (5.14)
где i – число цилиндров; n – частота вращения вала, мин-1; Vh в дм3;
· массовая, кг/ч:  Мц. (5.15)
Мц. (5.15)
Лопаточные компрессоры: процессы, протекающие в центробежном компрессоре; уравнения неразрывности, момента количества движения и энергии; особенности процессов в осевом компрессоре.
В основе расчета центробежного компрессора (рис. 5.4) лежат три основных уравнения: расхода, первого закона термодинамики для газового потока (уравнение энергии) и момента количества движения.
Из уравнения расхода  определяются площади проходных сечений и, соответственно, диаметры рабочего колеса, диффузора и выходного патрубка.
определяются площади проходных сечений и, соответственно, диаметры рабочего колеса, диффузора и выходного патрубка.
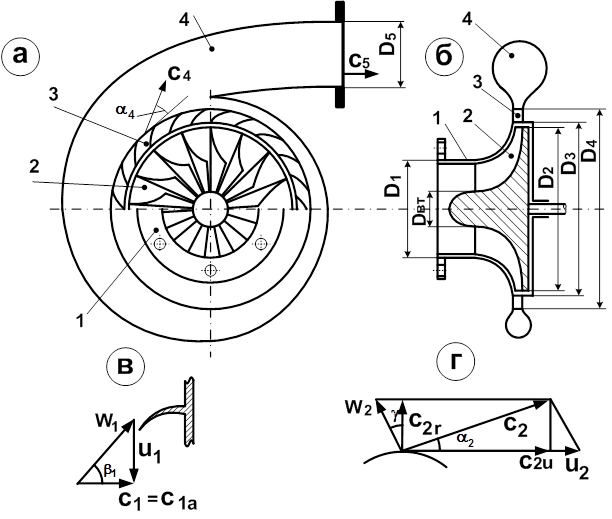


Рис. 5.4 Схема центробежного компрессора
а – вид спереди с поперечным разрезом; б – продольный разрез компрессора; в – треугольники скоростей на входе в рабочее колесо; г – треугольники скоростей на выходе из рабочего колеса; 1 – входной патрубок; 2 – рабочее колесо; 3 – диффузор;4 - выходной патрубок;  ,
,  – абсолютные скорости на входе в рабочее колесо и на выходе из него;
– абсолютные скорости на входе в рабочее колесо и на выходе из него;  – осевая составляющая абсолютной скорости на входе в рабочее колесо;
– осевая составляющая абсолютной скорости на входе в рабочее колесо;  ,
,  – окружная и радиальная составляющие абсолютной скорости на выходе из колеса;
– окружная и радиальная составляющие абсолютной скорости на выходе из колеса;  ,
, 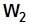 – относительные скорости газа на входе в рабочее колесо и выходе из него;
– относительные скорости газа на входе в рабочее колесо и выходе из него;  ,
,  – окружные скорости рабочего колеса на среднем радиусе на входе и на наружном радиусе на выходе;
– окружные скорости рабочего колеса на среднем радиусе на входе и на наружном радиусе на выходе;  – абсолютная скорость на выходе из диффузора;
– абсолютная скорость на выходе из диффузора;  – абсолютная скорость газа на выходе из компрессора.
– абсолютная скорость газа на выходе из компрессора.
Наружный диаметр колеса на входе вычисляется по выражению
 , (5.17)
, (5.17)
где G – секундный расход газа, кг/с;  – осевая составляющая абсолютной скорости на входе в колесо, (
– осевая составляющая абсолютной скорости на входе в колесо, (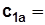 60…120 м/с);
60…120 м/с);  – конструктивный параметр (отношение диаметра втулки к наружному диаметру колеса на входе,
– конструктивный параметр (отношение диаметра втулки к наружному диаметру колеса на входе,  0,3…0,5).
0,3…0,5).
Диаметр втулки
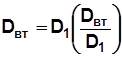 . (5.18)
. (5.18)
Уравнение энергии применяется для определения необходимой удельной работы при заданной степени повышения давления 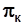 .
.
В адиабатном процессе сжатия
 , (5.19)
, (5.19)
с учетом потерь  , (5.20)
, (5.20)
где  - степень повышения давления в компрессоре;
- степень повышения давления в компрессоре;  – адиабатный к.п.д. компрессора.
– адиабатный к.п.д. компрессора.
Удельная работа определяется также по уравнению
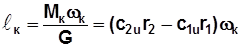 , (5.21)
, (5.21)
где Мк – крутящий момент, Н·м;  – угловая скорость рабочего колеса, 1/c.
– угловая скорость рабочего колеса, 1/c.
С учетом осевого входа воздуха в колесо (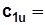 0) и соотношений
0) и соотношений  ,
, 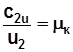 ;
;  следует уравнение связи удельной работы с параметрами рабочего колеса
следует уравнение связи удельной работы с параметрами рабочего колеса
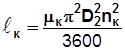 . (5.22)
. (5.22)
Из этого уравнения при заданной частоте вращения рабочего колеса  определяется наружный диаметр колеса
определяется наружный диаметр колеса
 . (5.23)
. (5.23)
В этих уравнениях  – коэффициент мощности;
– коэффициент мощности;  – окружная составляющая абсолютной скорости воздуха на выходе из рабочего колеса;
– окружная составляющая абсолютной скорости воздуха на выходе из рабочего колеса;  – окружная скорость на выходе из колеса.
– окружная скорость на выходе из колеса.
Мощность на привод компрессора (кВт)
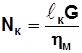 , (5.24)
, (5.24)
где  – удельная работа, кДж/кг; G – секундный расход газа, кг/с;
– удельная работа, кДж/кг; G – секундный расход газа, кг/с;  – механический к.п.д.
– механический к.п.д.
 2020-06-08
2020-06-08 308
308








