Задача 16 (демонстрационный вариант 2020 г.).
Задача 1
Две окружности касаются внешним образом в точке  Прямая
Прямая  касается первой окружности в точке
касается первой окружности в точке  , а второй — в точке
, а второй — в точке  Прямая
Прямая 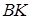 пересекает первую окружность в точке
пересекает первую окружность в точке  прямая
прямая  пересекает вторую окружность
пересекает вторую окружность
в точке 
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника 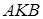 , если известно, что радиусы окружностей равны 4 и 1.
, если известно, что радиусы окружностей равны 4 и 1.
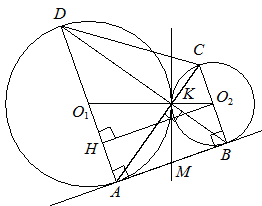
Решение. а) Обозначим центры окружностей  и
и  соответственно. Пусть общая касательная, проведённая
соответственно. Пусть общая касательная, проведённая
к окружностям в точке  пересекает
пересекает  в точке
в точке  По свойству касательных, проведённых из одной точки,
По свойству касательных, проведённых из одной точки, 
и  Треугольник AKB, у которого медиана равна половине стороны,
Треугольник AKB, у которого медиана равна половине стороны,
к которой она проведена, прямоугольный.
Вписанный угол  прямой, поэтому он опирается на диаметр
прямой, поэтому он опирается на диаметр  Значит,
Значит,  Аналогично, получаем, что
Аналогично, получаем, что  Следовательно, прямые AD и BC параллельны.
Следовательно, прямые AD и BC параллельны.
б) Пусть, для определённости, первая окружность имеет радиус 4, а вторая — радиус 1.
Треугольники  и
и  подобны,
подобны,  . Пусть
. Пусть  тогда
тогда

У треугольников AKD и AKB общая высота, следовательно,  то есть
то есть  Аналогично,
Аналогично, 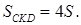 Площадь трапеции
Площадь трапеции  равна
равна  .
.
Вычислим площадь трапеции ABCD. Проведём к  перпендикуляр
перпендикуляр  равный высоте трапеции, и найдём его из прямоугольного треугольника
равный высоте трапеции, и найдём его из прямоугольного треугольника  :
:
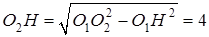 .
.
Тогда
 .
.
Следовательно, 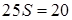 , откуда
, откуда  и
и 
Ответ: 3,2.
Задача 2
В трапеции  боковая сторона
боковая сторона  перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки  на сторону
на сторону  опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне  отмечена точка
отмечена точка  так, что прямые
так, что прямые  и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 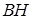 и
и  параллельны.
параллельны.
б) Найдите отношение 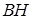 к
к  , если
, если  .
.
Решение.
а) Поскольку
 ,
около четырёхугольников ,
около четырёхугольников  и и  можно описать окружности (рис. 1).
Значит, можно описать окружности (рис. 1).
Значит,
 ,
то есть прямые ,
то есть прямые 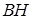 и и  параллельны. параллельны.
| 
|
б) Опустим из точки 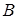 перпендикуляр перпендикуляр 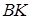 на прямую на прямую  (рис. 2). Стороны (рис. 2). Стороны  и и  треугольников треугольников  и и  лежат на одной прямой, а стороны лежат на одной прямой, а стороны 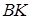 и и  , , 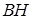 и и  попарно параллельны. Значит, треугольники попарно параллельны. Значит, треугольники  и и  подобны.
Поскольку подобны.
Поскольку

| 
|
коэффициент подобия равен  . Значит,
. Значит,
 .
.
Ответ: б)  .
.
Пример 1.
В трапеции  боковая сторона
боковая сторона  перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки  на сторону
на сторону  опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне  отмечена точка
отмечена точка  так, что прямые
так, что прямые  и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 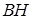 и
и  параллельны.
параллельны.
б) Найдите отношение 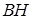 к
к  , если
, если  .
.
Ответ: б)  .
.

Комментарий.
Имеется попытка доказательства утверждения пункта а. Логическая ошибка содержится в записи 5) – при вычислении угла  :
:  . Замена угла
. Замена угла  углом
углом  возможна только при условии параллельности прямых
возможна только при условии параллельности прямых 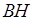 и
и  , а как раз это и требовалось доказать.
, а как раз это и требовалось доказать.
Оценка эксперта: 0 баллов.
Пример 2.
В трапеции  боковая сторона
боковая сторона  перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки  на сторону
на сторону  опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне  отмечена точка
отмечена точка  так, что прямые
так, что прямые  и
и  перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 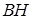 и
и  параллельны.
параллельны.
б) Найдите отношение 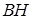 к
к  , если
, если  .
.
Ответ: б)  .
.


Комментарий.
В данном решении есть попытка доказательства утверждения пункта а. Логическая ошибка содержится в записи  – это возможно только при параллельности прямых
– это возможно только при параллельности прямых 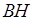 и
и  , а как раз это и требовалось доказать. Верный ответ в пункте б получен обоснованно с использованием недоказанного утверждения пункта а.
, а как раз это и требовалось доказать. Верный ответ в пункте б получен обоснованно с использованием недоказанного утверждения пункта а.
 2020-06-10
2020-06-10 74
74







